Question

已知cosx+cosy=1，则sinx-siny的取值范围是

1. A.
   [-1，1]
2. B.
   [-2，2]
3. C.
   
4. D.
   

Answer 1

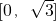
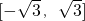
D
分析：可由（sinx-siny）²+（cosx+cosy）²=（sin²x+cos²x）+（sin²y+cos²y）+2（cosxcosy-sinxsiny）=2+2cos（x+y），再结合cosx+cosy=1，即可求得sinx-siny的取值范围．
解答：∵（sinx-siny）²+（cosx+cosy）²=（sin²x+cos²x）+（sin²y+cos²y）+2（cosxcosy-sinxsiny）
=2+2cos（x+y），
又∵cosx+cosy=1，
∴（sinx-siny）²=1+2cos（x+y）≤3．
∴-≤sinx-siny≤，即：sinx-siny的取值范围是[-，]．
故选D．
点评：本题考查同角三角函数间的基本关系，难点在于解题突破口（sinx-siny）²+（cosx+cosy）²=2+2cos（x+y）的选择，属于中档题．