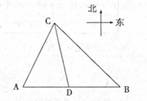
题目内容
 港口A北偏东30°方向的B处有一小岛,A正东方向的C处有一渔船,该渔船距岛B为31海里,现该渔船从C处沿着正西方向航行20海里到D处后出现机械故障最多只能航行12海里,此时测得渔船距离小岛B还有21海里,故只能继续向港口航去,问该渔船最终是否需要港口派船在海上救援?
港口A北偏东30°方向的B处有一小岛,A正东方向的C处有一渔船,该渔船距岛B为31海里,现该渔船从C处沿着正西方向航行20海里到D处后出现机械故障最多只能航行12海里,此时测得渔船距离小岛B还有21海里,故只能继续向港口航去,问该渔船最终是否需要港口派船在海上救援?分析:在△BCD中利用余弦定理,算出cos∠CDB=-
,结合同角三角函数关系得到sin∠CDB=
,再用差角的正弦公式算出sin∠BAD=
.最后在△ACD中用正弦定理,得到AD=15,说明渔船不能到岸,因此需要港口派船在海上救援.
| 1 |
| 7 |
4
| ||
| 7 |
5
| ||
| 14 |
解答:解:在△BCD中,BC=31,BD=21,CD=20
∴由余弦定理可得,cos∠CDB=
=-
∴sin∠CDB=
=
由此可得:sin∠BAD=sin(∠CDB-60°)=sin∠CDBcos60°-cos∠CDBsin60°=
在△ACD中,由正弦定理,可得
=
,
即
=
,解之得AD=15
∴渔船距港口还有15海里,无法到达港口,因此需要港口派船在海上救援.
∴由余弦定理可得,cos∠CDB=
| BD2+CD2-BC2 |
| 2BD•CD |
| 1 |
| 7 |
∴sin∠CDB=
| 1-cos2∠CDB |
4
| ||
| 7 |
由此可得:sin∠BAD=sin(∠CDB-60°)=sin∠CDBcos60°-cos∠CDBsin60°=
5
| ||
| 14 |
在△ACD中,由正弦定理,可得
| AD |
| sin∠BAD |
| BD |
| sin∠BAD |
即
| AD | ||||
|
| 21 | ||||
|
∴渔船距港口还有15海里,无法到达港口,因此需要港口派船在海上救援.
点评:本题给出实际应用问题,讨论渔船是否需要海上救援.着重考查了运用正余弦定理三角形及其实际应用等知识,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
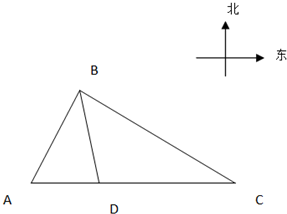
 港口A北偏东30°方向的C处有一检查站,港口正东方向的B处有一轮船,距离检查站为31海里,该轮船从B处沿正西方向航行20海里后到达D处观测站,已知观测站与检查站距离21海里,问此时轮船离港口A还有多远?
港口A北偏东30°方向的C处有一检查站,港口正东方向的B处有一轮船,距离检查站为31海里,该轮船从B处沿正西方向航行20海里后到达D处观测站,已知观测站与检查站距离21海里,问此时轮船离港口A还有多远? 港口A北偏东30°方向的C处有一检查站,港口正东方向的B处有一轮船,距离检查站为31海里,该轮船从B处沿正西方向航行20海里后到达D处观测站,已知观测站与检查站距离21海里,问检查站C离港口A有多远?
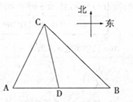
港口A北偏东30°方向的C处有一检查站,港口正东方向的B处有一轮船,距离检查站为31海里,该轮船从B处沿正西方向航行20海里后到达D处观测站,已知观测站与检查站距离21海里,问检查站C离港口A有多远?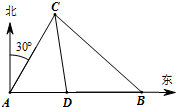 如图所示,港口A北偏东30°方向的点C处有一观测站,港口正东方向的B处有一轮船,测得BC为31海里.该轮船从B处沿正西方向航行20海里后到达D处,测得CD为21海里.问此时轮船离港口A还有多少海里?
如图所示,港口A北偏东30°方向的点C处有一观测站,港口正东方向的B处有一轮船,测得BC为31海里.该轮船从B处沿正西方向航行20海里后到达D处,测得CD为21海里.问此时轮船离港口A还有多少海里?