题目内容
已知函数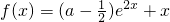 .(a∈R)
.(a∈R)
(Ⅰ)若f(x)在区间(-∞,0)上单调递增,求实数a的取值范围;
(Ⅱ)若在区间(0,+∞)上,函数f(x)的图象恒在曲线y=2aex下方,求a的取值范围.
解:(Ⅰ)f(x)在区间(-∞,0)上单调递增,
则f'(x)=(2a-1)e2x+1≥0在区间(-∞,0)上恒成立.
即 ,而当x∈(-∞,0)时,
,而当x∈(-∞,0)时, ,故1-2a≤1.
,故1-2a≤1.
∴a≥0.
(Ⅱ)令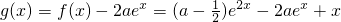 ,定义域为R.
,定义域为R.
在区间(0,+∞)上,函数f(x)的图象恒在曲线y=2aex下方等价于g(x)<0在区间(0,+∞)上恒成立.
∵g'(x)=(2a-1)e2x-2aex+1=(ex-1)[(2a-1)ex-1],
①若 ,令g'(x)=0,得极值点x1=0,
,令g'(x)=0,得极值点x1=0,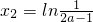 ,
,
当x2>x1=0,即 时,在(x2,+∞)上有g'(x)>0,此时g(x)在区间(x2,+∞)上是增函数,并且在该区间上有g(x)∈(g(x2),+∞),不合题意;
时,在(x2,+∞)上有g'(x)>0,此时g(x)在区间(x2,+∞)上是增函数,并且在该区间上有g(x)∈(g(x2),+∞),不合题意;
当x2≤x1=0,即a≥1时,同理可知,g(x)在区间(0,+∞)上,
有g(x)∈(g(0),+∞),也不合题意;
②若 ,则有2a-1≤0,此时在区间(0,+∞)上恒有g'(x)<0,从而g(x)在区间(0,+∞)上是减函数;
,则有2a-1≤0,此时在区间(0,+∞)上恒有g'(x)<0,从而g(x)在区间(0,+∞)上是减函数;
要使g(x)<0在此区间上恒成立,只须满足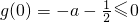
 ,
,
由此求得a的范围是 .
.
综合①②可知,当 时,函数f(x)的图象恒在直线y=2aex下方.
时,函数f(x)的图象恒在直线y=2aex下方.
分析:(I)f(x)在区间(-∞,0)上单调递增?f'(x)=(2a-1)e2x+1≥0在区间(-∞,0)上恒成立,通过分离参数,利用指数函数的单调性即可得出;
(II)令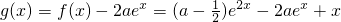 ,定义域为R.则在区间(0,+∞)上,函数f(x)的图象恒在曲线y=2aex下方?g(x)<0在区间(0,+∞)上恒成立.利用导数研究函数g(x)的单调性,通过对a分类讨论即可得出.
,定义域为R.则在区间(0,+∞)上,函数f(x)的图象恒在曲线y=2aex下方?g(x)<0在区间(0,+∞)上恒成立.利用导数研究函数g(x)的单调性,通过对a分类讨论即可得出.
点评:本题主要考查函数的基本性质、导数的概念、利用导数研究函数的单调性等基础知识和基本方法,同时考查逻辑推理能力和分类讨论的思想方法.
则f'(x)=(2a-1)e2x+1≥0在区间(-∞,0)上恒成立.
即
 ,而当x∈(-∞,0)时,
,而当x∈(-∞,0)时, ,故1-2a≤1.
,故1-2a≤1. ∴a≥0.
(Ⅱ)令
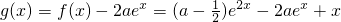 ,定义域为R.
,定义域为R.在区间(0,+∞)上,函数f(x)的图象恒在曲线y=2aex下方等价于g(x)<0在区间(0,+∞)上恒成立.
∵g'(x)=(2a-1)e2x-2aex+1=(ex-1)[(2a-1)ex-1],
①若
 ,令g'(x)=0,得极值点x1=0,
,令g'(x)=0,得极值点x1=0,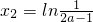 ,
,当x2>x1=0,即
 时,在(x2,+∞)上有g'(x)>0,此时g(x)在区间(x2,+∞)上是增函数,并且在该区间上有g(x)∈(g(x2),+∞),不合题意;
时,在(x2,+∞)上有g'(x)>0,此时g(x)在区间(x2,+∞)上是增函数,并且在该区间上有g(x)∈(g(x2),+∞),不合题意;当x2≤x1=0,即a≥1时,同理可知,g(x)在区间(0,+∞)上,
有g(x)∈(g(0),+∞),也不合题意;
②若
 ,则有2a-1≤0,此时在区间(0,+∞)上恒有g'(x)<0,从而g(x)在区间(0,+∞)上是减函数;
,则有2a-1≤0,此时在区间(0,+∞)上恒有g'(x)<0,从而g(x)在区间(0,+∞)上是减函数;要使g(x)<0在此区间上恒成立,只须满足
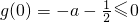
 ,
,由此求得a的范围是
 .
. 综合①②可知,当
 时,函数f(x)的图象恒在直线y=2aex下方.
时,函数f(x)的图象恒在直线y=2aex下方.分析:(I)f(x)在区间(-∞,0)上单调递增?f'(x)=(2a-1)e2x+1≥0在区间(-∞,0)上恒成立,通过分离参数,利用指数函数的单调性即可得出;
(II)令
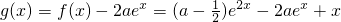 ,定义域为R.则在区间(0,+∞)上,函数f(x)的图象恒在曲线y=2aex下方?g(x)<0在区间(0,+∞)上恒成立.利用导数研究函数g(x)的单调性,通过对a分类讨论即可得出.
,定义域为R.则在区间(0,+∞)上,函数f(x)的图象恒在曲线y=2aex下方?g(x)<0在区间(0,+∞)上恒成立.利用导数研究函数g(x)的单调性,通过对a分类讨论即可得出.点评:本题主要考查函数的基本性质、导数的概念、利用导数研究函数的单调性等基础知识和基本方法,同时考查逻辑推理能力和分类讨论的思想方法.

练习册系列答案
相关题目
 ,其中a∈R.
,其中a∈R.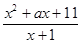 (a∈R),若对于任意的X∈N*,f(x)≥3恒成立,则a的取值范围是___
(a∈R),若对于任意的X∈N*,f(x)≥3恒成立,则a的取值范围是___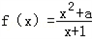 (其中a∈R).
(其中a∈R).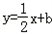 ,求实数a,b的值;
,求实数a,b的值;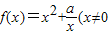 ,常数a∈R),若函数f(x)在x∈[2,+∞)上是增函数,则a的取值范围是 .
,常数a∈R),若函数f(x)在x∈[2,+∞)上是增函数,则a的取值范围是 .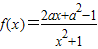 ,其中a∈R.
,其中a∈R.