题目内容
已知点 ,
,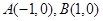 ,直线
,直线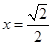 上有两个动点
上有两个动点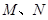 ,始终使
,始终使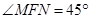 ,三角形
,三角形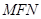 的外心轨迹为曲线
的外心轨迹为曲线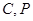 为曲线
为曲线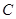 在一象限内的动点,设
在一象限内的动点,设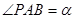 ,
,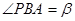 ,
,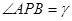 ,则( )
,则( )
 ,
,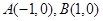 ,直线
,直线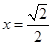 上有两个动点
上有两个动点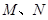 ,始终使
,始终使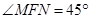 ,三角形
,三角形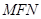 的外心轨迹为曲线
的外心轨迹为曲线 为曲线
为曲线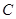 在一象限内的动点,设
在一象限内的动点,设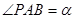 ,
,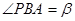 ,
,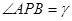 ,则( )
,则( )A.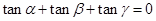 | B.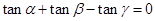 |
C.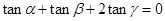 | D. |
C
试题分析:依题意设
 ,
, 的外心为
的外心为 ,则有
,则有 即
即 ,又由
,又由 得
得 即
即 ,将
,将 代入化简得
代入化简得 即
即 ,在
,在 中,由余弦定理可得
中,由余弦定理可得 即
即
展开整理得
 即
即
也就是
 ,将
,将 、
、 代入可得
代入可得 ,整理可得
,整理可得 ,即
,即 的外心轨迹方程为
的外心轨迹方程为
设
 ,则
,则 即
即 ,而
,而
又
 ,所以
,所以
所以
 ,故选C.
,故选C.
练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
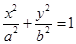 (a>b>0),过点(0,1),且离心率为
(a>b>0),过点(0,1),且离心率为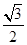 .
.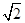 与x轴交于点D,点P是椭圆C上异于A,B的动点,直线AP,BP分别交直线l于E,F两点.证明:当点P在椭圆C上运动时,
与x轴交于点D,点P是椭圆C上异于A,B的动点,直线AP,BP分别交直线l于E,F两点.证明:当点P在椭圆C上运动时,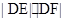 恒为定值.
恒为定值.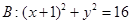 ,C为圆B上任意一点,求AC垂直平分线与线段BC的交点P的轨迹方程。
,C为圆B上任意一点,求AC垂直平分线与线段BC的交点P的轨迹方程。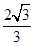 ).过点P(1,1)分别作斜率为k1,k2的椭圆的动弦AB,CD,设M,N分别为线段AB,CD的中点.
).过点P(1,1)分别作斜率为k1,k2的椭圆的动弦AB,CD,设M,N分别为线段AB,CD的中点.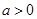 ,向量
,向量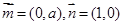 ,经过定点
,经过定点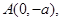 以
以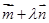 为方向向量的直线与经过定点
为方向向量的直线与经过定点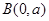 以
以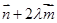 为方向向量的直线相交于
为方向向量的直线相交于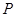 ,其中
,其中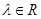 ,
,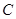 的方程;(2)若
的方程;(2)若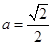 ,过
,过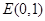 的直线交曲线
的直线交曲线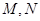 两点,求
两点,求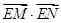 的取值范围。
的取值范围。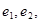 则
则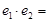 ______.
______.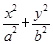 =1(a>b>0)的离心率e=
=1(a>b>0)的离心率e=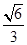 ,一条准线方程为x=
,一条准线方程为x=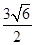
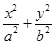 =1(a>b>0)的左、右焦点,A是椭圆C的顶点,B是直线AF2与椭圆C的另一个交点,∠F1AF2=60°.
=1(a>b>0)的左、右焦点,A是椭圆C的顶点,B是直线AF2与椭圆C的另一个交点,∠F1AF2=60°.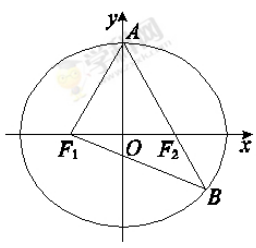
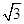 ,求a,b的值.
,求a,b的值.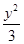 =1.
=1.