题目内容
9.已知函数$f(x)=lo{g}_{a}x+lo{g}_{\frac{1}{a}}$8(a>0,且a≠1),在集合{$\frac{1}{4}$,$\frac{1}{3}$,$\frac{1}{2}$,3,4,5,6,7}中任取一个数为a,则f(3a+1)>f(2a)>0的概率为( )| A. | $\frac{1}{4}$ | B. | $\frac{3}{8}$ | C. | $\frac{1}{2}$ | D. | $\frac{3}{4}$ |
分析 由f(x)=logax-loga8)=$lo{g}_{a}\frac{x}{8}$,求出基本事件总数和满足f(3a+1)>f(2a)>0的基本事件个数,由此能示出f(3a+1)>f(2a)>0的概率.
解答 解:∵函数$f(x)=lo{g}_{a}x+lo{g}_{\frac{1}{a}}$8(a>0,且a≠1),
∴f(x)=logax-loga8)=$lo{g}_{a}\frac{x}{8}$,
∵在集合{$\frac{1}{4}$,$\frac{1}{3}$,$\frac{1}{2}$,3,4,5,6,7}中任取一个数为a,
∴基本事件总数n=8,
∵f(3a+1)>f(2a)>0
3a+1-2a=a-1,
当a>1时,3a+1>2a,2a>1,即a=5,6,7时才成立;
当a<1时,3a+1<2a,即a+1<1,不成立.
∴满足f(3a+1)>f(2a)>0的基本事件个数m=3,
∴f(3a+1)>f(2a)>0的概率为p=$\frac{m}{n}=\frac{3}{8}$.
点评 本题考查概率的求法,是基础题,解题时要认真审题,注意等可能事件概率计算公式的合理运用.

练习册系列答案
 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案
相关题目
3.集合A={1,2,3,4},B={x|3≤x<6},则A∩B=( )
| A. | {3,4} | B. | {4} | C. | { x|3≤x≤4} | D. | ∅ |
4.设a=30.4,b=log30.4,c=0.43,则a,b,c的大小关系为( )
| A. | a>c>b | B. | a>b>c | C. | c>a>b | D. | c>b>a |
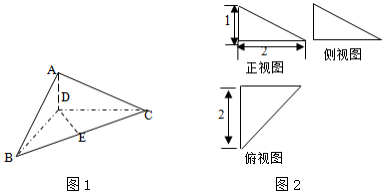
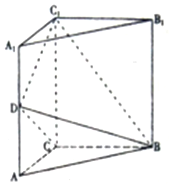 如图,三棱柱ABC-A1B1C1中,侧棱垂直底面,∠ACB=90°,AC=BC=$\frac{1}{2}A{A_1}$=2,点D是棱AA1的中点.
如图,三棱柱ABC-A1B1C1中,侧棱垂直底面,∠ACB=90°,AC=BC=$\frac{1}{2}A{A_1}$=2,点D是棱AA1的中点.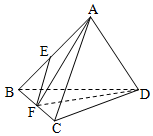 在正四面体ABCD中,点E,F分别是AB,BC的中点,则下列命题正确的序号是①③④
在正四面体ABCD中,点E,F分别是AB,BC的中点,则下列命题正确的序号是①③④