题目内容
已知函数f(x)=|2x-1|+|x-2a|
(Ⅰ)当a=-
时,求不等式f(x)>2的解集;
(Ⅱ)若当x∈[1,2]时,f(x)≤3恒成立,则实数a的值.
(Ⅰ)当a=-
| 1 |
| 2 |
(Ⅱ)若当x∈[1,2]时,f(x)≤3恒成立,则实数a的值.
考点:绝对值不等式的解法
专题:计算题,函数的性质及应用,不等式的解法及应用
分析:(Ⅰ)运用零点分区间的方法,讨论当x>
时,当-1≤x≤
时,当x<-1时,去掉绝对值,分别解不等式,再求并集即可;
(Ⅱ)由题意,f(x)≤3可化为|x-2a|≤3-|2x-1|,由x∈[1,2],得|x-2a|≤4-2x,即3x-4≤2a≤4-x 对x∈[1,2]恒成立,在x∈[1,2]时,求得3x-4 的最大值和4-x的最小值,即得a的值.
| 1 |
| 2 |
| 1 |
| 2 |
(Ⅱ)由题意,f(x)≤3可化为|x-2a|≤3-|2x-1|,由x∈[1,2],得|x-2a|≤4-2x,即3x-4≤2a≤4-x 对x∈[1,2]恒成立,在x∈[1,2]时,求得3x-4 的最大值和4-x的最小值,即得a的值.
解答:
解:(Ⅰ)当a=-
时,不等式f(x)>2即为
|2x-1|+|x+1|>2,
当x>
时,2x-1+x+1>2,解得x>
,则有x>
;
当-1≤x≤
时,1-2x+x+1>2解得x<0,则有-1≤x<0;
当x<-1时,1-2x-x-1>2解得x<-
,则有x<-1.
综上可得,x>
或x<0.
则解集为{x|x>
或x<0};
(Ⅱ)∵f(x)=|2x-1|+|x-2a|,且f(x)≤3,
∴|x-2a|≤3-|2x-1|,
又∵x∈[1,2],∴|x-2a|≤4-2x,
即 2x-4≤2a-x≤4-2x,
∴3x-4≤2a≤4-x对x∈[1,2]恒成立,
当1≤x≤2时,3x-4的最大值2,4-x的最小值为2,
∴2≤2a≤2,即有a=1.
| 1 |
| 2 |
|2x-1|+|x+1|>2,
当x>
| 1 |
| 2 |
| 2 |
| 3 |
| 2 |
| 3 |
当-1≤x≤
| 1 |
| 2 |
当x<-1时,1-2x-x-1>2解得x<-
| 2 |
| 3 |
综上可得,x>
| 2 |
| 3 |
则解集为{x|x>
| 2 |
| 3 |
(Ⅱ)∵f(x)=|2x-1|+|x-2a|,且f(x)≤3,
∴|x-2a|≤3-|2x-1|,
又∵x∈[1,2],∴|x-2a|≤4-2x,
即 2x-4≤2a-x≤4-2x,
∴3x-4≤2a≤4-x对x∈[1,2]恒成立,
当1≤x≤2时,3x-4的最大值2,4-x的最小值为2,
∴2≤2a≤2,即有a=1.
点评:本题考查了含有绝对值不等式的解法问题,解题时应利用等价转化、分类讨论的数学思想,考查不等式的恒成立问题,注意转化为求函数的最值,是中档题.

练习册系列答案
相关题目
等比数列{an}中,前n项和Sn=
+x,则x的值为( )
| 2n |
| 4 |
A、-
| ||
| B、-4 | ||
| C、-1 | ||
| D、4 |
等比数列{an}中,首项a1=2,公比为3,Sn为其前n项和,则S4+a3等于( )
| A、44 | B、64 | C、98 | D、134 |
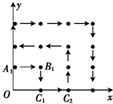 为防洪抗旱,某地区大面积植树造林,如图,在区域{(x,y)|x≥0,y≥0}内植树,第一棵树在A1(0,1)点,第二棵树在B1(1,1)点,第三棵树在C1(1,0)点,第四棵树在C2(2,0)点,接着按图中箭头方向每隔一个单位长度种一棵树,那么,坐标为(43,0)的点是第
为防洪抗旱,某地区大面积植树造林,如图,在区域{(x,y)|x≥0,y≥0}内植树,第一棵树在A1(0,1)点,第二棵树在B1(1,1)点,第三棵树在C1(1,0)点,第四棵树在C2(2,0)点,接着按图中箭头方向每隔一个单位长度种一棵树,那么,坐标为(43,0)的点是第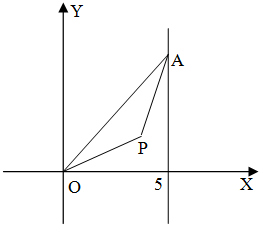 如图,点A在直线x=5上移动,等腰△OPA的顶角∠OPA为120°(O,P,A按逆时针方向排列),求点P的轨迹方程.
如图,点A在直线x=5上移动,等腰△OPA的顶角∠OPA为120°(O,P,A按逆时针方向排列),求点P的轨迹方程.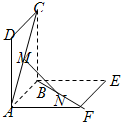 如图,已知四边形ABCD,ABEF都是矩形,M、N分别是对角线AC和BF的中点,则MN与平面BCE的关系是
如图,已知四边形ABCD,ABEF都是矩形,M、N分别是对角线AC和BF的中点,则MN与平面BCE的关系是