题目内容
20.设函数f(x)=|x-a|+|x-2|.(1)当a=2时,求不等式f(x)≤14的解集;
(2)若f(x)≥a2对x∈R恒成立,求实数a的取值范围.
分析 (1)先将不等式等价为:|x-2|≤7,再直接去绝对值求解;
(2)先用绝对值三角不等式将问题等价为:f(x)min=|a-2|≥a2,再分类讨论求解即可.
解答 解:(1)当a=2时,不等式f(x)≤14即为,|x-2|+|x-2|≤14,
所以,|x-2|≤7,不等式等价为:-7≤x-2≤7,
解得,-5≤x≤9,
故原不等式的解集为:{x|-5≤x≤9};
(2)因为不等式f(x)≥a2对x∈R恒成立,
所以,f(x)min≥a2,
根据绝对值三角不等式,|x-a|+|x-2|≥|(x-a)-(x-2)|=|a-2|,
即f(x)min=|a-2|,所以,|a-2|≥a2,分类讨论如下:
①当a≥2时,a-2≥a2,无解;
②当a<2时,2-a≥a2,解得a∈[-2,1],
综合以上讨论得,实数a的取值范围为:[-2,1].
点评 本题主要考查了绝对值不等式的解法,以及绝对值三角不等式的应用和不等式恒成立问题的求解,体现了分类讨论的解题思想,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
10.空间中,如果两个角的两条边分别对应平行,那么这两个角( )
| A. | 相等 | B. | 互补 | C. | 相等或互补 | D. | 不能确定 |
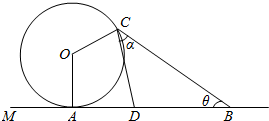 如图,在一条景观道的一端有一个半径为50米的圆形摩天轮O,逆时针15分钟转一圈,从A处进入摩天轮的座舱,OA垂直于地面AM,在距离A处150米处设置了一个望远镜B.
如图,在一条景观道的一端有一个半径为50米的圆形摩天轮O,逆时针15分钟转一圈,从A处进入摩天轮的座舱,OA垂直于地面AM,在距离A处150米处设置了一个望远镜B. 试根据流程图回答:
试根据流程图回答: