题目内容
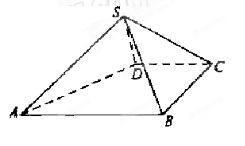
如图,四棱锥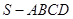 中,
中,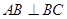 ,
,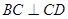 ,侧面
,侧面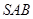 为等边三角形,
为等边三角形,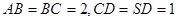 .
.
(Ⅰ)证明: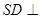 平面
平面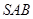 ;
;
(Ⅱ)求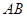 与平面
与平面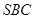 所成角的正弦值.
所成角的正弦值.
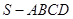 中,
中,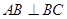 ,
,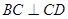 ,侧面
,侧面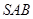 为等边三角形,
为等边三角形,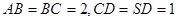 .
.
(Ⅰ)证明:
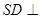 平面
平面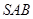 ;
;(Ⅱ)求
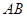 与平面
与平面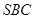 所成角的正弦值.
所成角的正弦值. (Ⅰ)见解析(Ⅱ)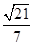
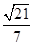
本试题主要是考查了线面垂直的问题和线面角的求解的综合运用。
(1)要证明线面垂直关键是证明线线垂直,BA垂直于平面ASD。
(2)利用等价转化思想,通过求解点到面的距离得到线面角的求解。
解:
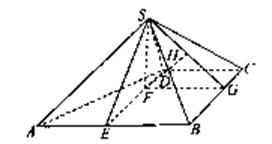
(I)取AB中点E,连结DE,则四边形BCDE为矩形,DE=CB=2,
连结SE,则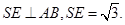
又SD=1,故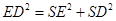 ,
,
所以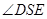 为直角。 …………3分
为直角。 …………3分
由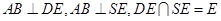 ,
,
得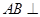 平面SDE,所以
平面SDE,所以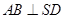 。
。
SD与两条相交直线AB、SE都垂直。
所以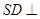 平面SAB。 …………6分
平面SAB。 …………6分
(II)由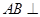 平面SDE知,
平面SDE知,
平面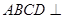 平面SED。
平面SED。
作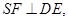 垂足为F,则SF
垂足为F,则SF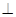 平面ABCD,
平面ABCD,
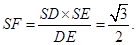
作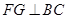 ,垂足为G,则FG=DC=1。
,垂足为G,则FG=DC=1。
连结SG,则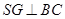 ,
,
又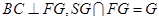 ,
,
故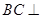 平面SFG,平面SBC
平面SFG,平面SBC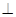 平面SFG。
平面SFG。
作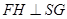 ,H为垂足,则
,H为垂足,则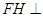 平面SBC。
平面SBC。
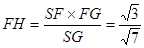 ,即F到平面SBC的距离为
,即F到平面SBC的距离为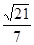 …………………………10分
…………………………10分
由于ED//BC,所以ED//平面SBC,E到平面SBC的距离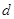 也有
也有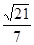
设AB与平面SBC所成的角为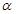 ,
,
则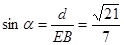 。………………………12分
。………………………12分
(1)要证明线面垂直关键是证明线线垂直,BA垂直于平面ASD。
(2)利用等价转化思想,通过求解点到面的距离得到线面角的求解。
解:

(I)取AB中点E,连结DE,则四边形BCDE为矩形,DE=CB=2,
连结SE,则
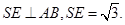
又SD=1,故
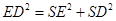 ,
,所以
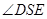 为直角。 …………3分
为直角。 …………3分由
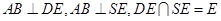 ,
,得
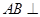 平面SDE,所以
平面SDE,所以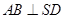 。
。SD与两条相交直线AB、SE都垂直。
所以
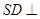 平面SAB。 …………6分
平面SAB。 …………6分(II)由
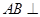 平面SDE知,
平面SDE知,平面
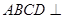 平面SED。
平面SED。作
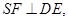 垂足为F,则SF
垂足为F,则SF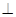 平面ABCD,
平面ABCD,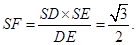
作
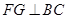 ,垂足为G,则FG=DC=1。
,垂足为G,则FG=DC=1。连结SG,则
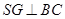 ,
,又
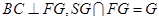 ,
,故
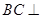 平面SFG,平面SBC
平面SFG,平面SBC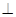 平面SFG。
平面SFG。作
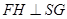 ,H为垂足,则
,H为垂足,则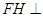 平面SBC。
平面SBC。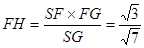 ,即F到平面SBC的距离为
,即F到平面SBC的距离为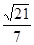 …………………………10分
…………………………10分由于ED//BC,所以ED//平面SBC,E到平面SBC的距离
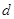 也有
也有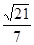
设AB与平面SBC所成的角为
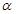 ,
,则
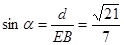 。………………………12分
。………………………12分
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
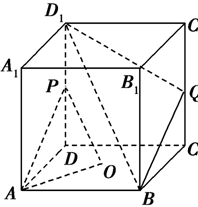
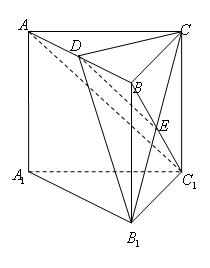
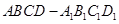 中,
中,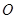 为底面
为底面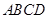 的中心,
的中心,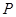 是
是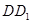 的中点,设
的中点,设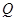 是
是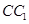 上的中点,求证:(1)
上的中点,求证:(1)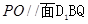 ;
;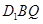 ∥平面
∥平面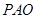 .
.
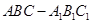 中,
中,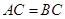 ,点
,点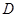 是
是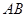 的中点,
的中点,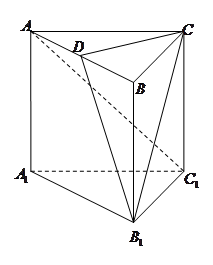
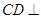 平面
平面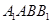 ;
;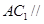 平面
平面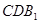
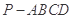 的底面是正方形,
的底面是正方形, ,点E在棱PB上.
,点E在棱PB上.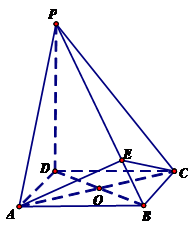
 ;
; 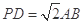 且
且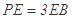 时,求AE与平面PDB所成的角的正切值.
时,求AE与平面PDB所成的角的正切值.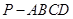 的底面为正方形,侧棱
的底面为正方形,侧棱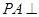 底面
底面 ,且
,且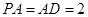 ,
,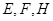 分别是线段
分别是线段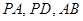 的中点.
的中点.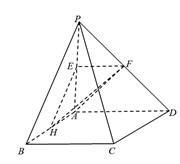
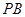 //平面
//平面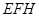 ;
;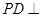 平面
平面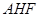 ;
;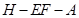 的大小.
的大小.
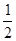 AB=1,M是PB的中点
AB=1,M是PB的中点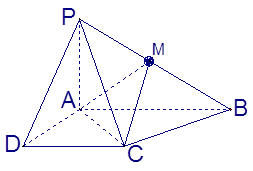
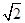 C.1 D.
C.1 D.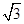
 ,
,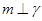 ,那么必有( )
,那么必有( )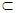 α,b
α,b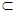 β α∥β
β α∥β