题目内容
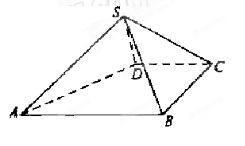
如图,四棱锥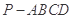 的底面是正方形,
的底面是正方形, ,点E在棱PB上.
,点E在棱PB上.
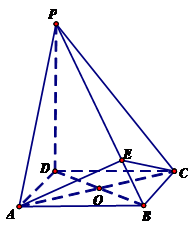
(Ⅰ)求证:平面 ;
;
(Ⅱ)当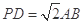 且
且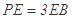 时,求AE与平面PDB所成的角的正切值.
时,求AE与平面PDB所成的角的正切值.
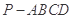 的底面是正方形,
的底面是正方形, ,点E在棱PB上.
,点E在棱PB上.
(Ⅰ)求证:平面
 ;
; (Ⅱ)当
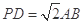 且
且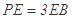 时,求AE与平面PDB所成的角的正切值.
时,求AE与平面PDB所成的角的正切值.(Ⅰ)见解析;(Ⅱ)AE与平面PDB所成的角的正切值为

本题考查空间直线线、平面的关系以及线面角的求法。注重将空间图形转化为平面图形处理的方法,注意传统方法求线面角的步骤:作---证---求。
解:(Ⅰ)∵四边形ABCD是正方形,∴AC⊥BD,∵ ,∴PD⊥AC,
,∴PD⊥AC,
∴AC⊥平面PDB,∴ .
.
(Ⅱ)设AC∩BD=O,连接OE,由(Ⅰ)知AC⊥平面PDB于O,
∴∠AEO为AE与平面PDB所的角。
设


 ,
,
 ,
,
 ,
, 
即AE与平面PDB所成的角的正切值为 .
.
解:(Ⅰ)∵四边形ABCD是正方形,∴AC⊥BD,∵
 ,∴PD⊥AC,
,∴PD⊥AC,∴AC⊥平面PDB,∴
 .
.(Ⅱ)设AC∩BD=O,连接OE,由(Ⅰ)知AC⊥平面PDB于O,
∴∠AEO为AE与平面PDB所的角。
设



 ,
,
 ,
,
 ,
, 
即AE与平面PDB所成的角的正切值为
 .
.
练习册系列答案
 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目
 的底面
的底面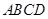 为矩形,且
为矩形,且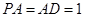 ,
,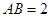 ,
,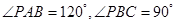 ,
,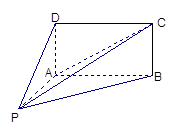
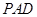 与平面
与平面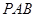 是否垂直?并说明理由;
是否垂直?并说明理由;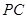 与平面
与平面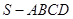 中,
中,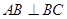 ,
,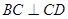 ,侧面
,侧面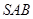 为等边三角形,
为等边三角形,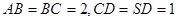 .
.
 平面
平面 与平面
与平面 所成角的正弦值.
所成角的正弦值.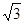 ,点F是PB的中点,点E在边BC上移动.
,点F是PB的中点,点E在边BC上移动.
 ,M是AB的中点,
,M是AB的中点,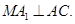
 平面ABC;
平面ABC;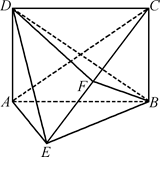
 底面ABCD,
底面ABCD, DAB为直角,AB‖CD,AD=CD=2AB,E、F分别为PC、CD的中点.
DAB为直角,AB‖CD,AD=CD=2AB,E、F分别为PC、CD的中点.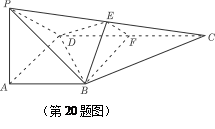
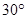 ,求k的取值范围.
,求k的取值范围.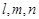 表示不同的直线,
表示不同的直线,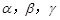 表示不同的平面,给出下列四个命题:
表示不同的平面,给出下列四个命题: 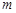 ∥
∥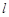 ,且
,且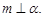 则
则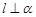 ;
; 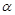 .则
.则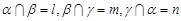 ,则
,则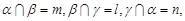 且n∥
且n∥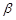 ,则
,则