题目内容
某高校在上学期依次举行了“法律、环保、交通”三次知识竞赛活动,要求每位同学至少参加一次活动.该高校2014级某班50名学生在上学期参加该项活动的次数统计如图所示.
(1)从该班中任意选两名学生,求他们参加活动次数不相等的概率.
 (2)从该班中任意选两名学生,用
(2)从该班中任意选两名学生,用 表示这两人参加活动次数之差的绝对值,求随机变量
表示这两人参加活动次数之差的绝对值,求随机变量 的分布列及数学期望
的分布列及数学期望 .
.
(3)从该班中任意选两名学生,用 表示
表示
这两人参加活动次数之和,记“函数
 在区间(3,5)上有且
在区间(3,5)上有且
只有一个零点”为事件A,求事件A发生的概率.
.解:(1)从该班任取两名学生,他们参加活动的次数恰好相等的概率:
P =  =
=  ,故P = 1 -
,故P = 1 -  =
=  .-----4分
.-----4分
(2) 从该班中任选两名学生,用x表示这两学生参加活动次数之差的绝对值,则x的可能取值分别为:0 ,1,2,
于是P(x = 0)=  , P(x = 1)=
, P(x = 1)=  =
=  ,
,
P(x = 2)=  =
=  , 从而x的分布列为:
, 从而x的分布列为:
| x | 0 | 1 | 2 |
| P | |
|
|
Ex = 0´ + 1´
+ 1´  + 2´
+ 2´  =
=  .---------------8分
.---------------8分
(3) 因为函数f(x) = x2 - hx – 1 在区间(3,5)上有且只有一个零点,则
f(3)×f(5) < 0 , 即:(8 - 3h)(24- 5h) < 0 , 
 < h <
< h <  -------10分
-------10分
又由于h的取值分别为:2,3,4,5,6,故h = 3或4,
故所求的概率为:P(A)=  =
=  .------------------12分
.------------------12分

练习册系列答案
相关题目
 的最小正周期为
的最小正周期为 ,最小值为
,最小值为 ,将函数
,将函数 的图像向左平移
的图像向左平移 (
( ,则
,则 B.
B. C.
C. D.
D.
 ,
, ,
, 为两个定点,
为两个定点,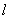 是⊙O的一条切线,若过A,B两点的抛 物线以直线
是⊙O的一条切线,若过A,B两点的抛 物线以直线 C.椭圆 D.抛物线
C.椭圆 D.抛物线




 ,则
,则 展开式中的常数项为_____
展开式中的常数项为_____ 的参数方程是
的参数方程是 ,圆C的极坐标方程为
,圆C的极坐标方程为 .
. =3125,
=3125, =15625,
=15625, =78125,…,则
=78125,…,则 的末四位数字为( )
的末四位数字为( ) 为可导函数,且满足
为可导函数,且满足 ,则过曲线
,则过曲线 上点
上点 处的切线斜率为
处的切线斜率为  .
.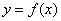 在点
在点 处的切线方程;
处的切线方程; 为曲线
为曲线