题目内容
已知双曲线x2-2y2=2的左、右焦点分别是F1、F2,动点P满足|PF1|+|PF2|=4.
(1)求动点P的轨迹E的过程.
(2)设过点F2且不垂直与坐标轴的动直线a交轨迹E与A、B两点,试问在y轴上是否存在一点D使得以DA、DB为邻边的平行四边形为菱形?若存在,试判断点D的活动范围:若不存在,试说明理由.
解:(1)双曲线的方程可化为 -y2=1,则|FF2|=2
-y2=1,则|FF2|=2 ,|PF1|+|PF2|=4>|FF2|,
,|PF1|+|PF2|=4>|FF2|,
所以点P的轨迹E是以F1,F2为焦点且长轴长为4的椭圆,其方程为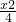 +y2=1.(3分)
+y2=1.(3分)
(2)假设存在满足条件的点D(0,m),设直线a的方程为y=k(x- )(k≠0)
)(k≠0)
代入椭圆方程得:(1+4k2)x2-8 k2x+12k2-4=0,
k2x+12k2-4=0,
设A(x1,y1),B(x2,y2),由韦达定理得:x1+x2= ,y1+y2=k(x1+x2-2
,y1+y2=k(x1+x2-2 )=
)=
 =(x1,y1-m),
=(x1,y1-m),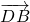 =(x2,y2-m),
=(x2,y2-m),
 =( x1+x2,y1+y2-2m),(6分)
=( x1+x2,y1+y2-2m),(6分)
又 =λ(1,k) (λ=x2-x1),
=λ(1,k) (λ=x2-x1),
∵以DA、DB为邻边的平行四边形为菱形,∴( +
+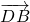 )⊥
)⊥
∴( +
+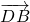 )•
)• =0,即
=0,即 +
+ -2mk=0,整理得:
-2mk=0,整理得: -2mk=0,(8分)
-2mk=0,(8分)
∵k≠0,∴m= =
=
若k>0,则 ≤
≤ (当且仅当k=
(当且仅当k= 时取等号),即m∈(0,
时取等号),即m∈(0, ](10分)
](10分)
若k<0,则 ≥-
≥- (当且仅当k=-
(当且仅当k=- 时取等号),即m∈[-
时取等号),即m∈[- ,0)(11分)
,0)(11分)
综上,满足条件的点D存在,其活动范围是满足- ≤y≤
≤y≤ 且y≠0的区域.
且y≠0的区域.
分析:(1)双曲线的方程可化为 -y2=1,则|FF2|=2
-y2=1,则|FF2|=2 ,|PF1|+|PF2|=4>|FF2|,由此知点P的轨迹E是以F1,F2为焦点且长轴长为4的椭圆,并能求出其方程.
,|PF1|+|PF2|=4>|FF2|,由此知点P的轨迹E是以F1,F2为焦点且长轴长为4的椭圆,并能求出其方程.
(2)假设存在满足条件的点D(0,m),设直线a的方程为y=k(x- ),代入椭圆方程得:(1+4k2)x2-8
),代入椭圆方程得:(1+4k2)x2-8 k2x+12k2-4=0,再由韦达定理结合分类讨论思想能够推导出满足条件的点D存在,其活动范围是满足-
k2x+12k2-4=0,再由韦达定理结合分类讨论思想能够推导出满足条件的点D存在,其活动范围是满足- ≤y≤
≤y≤ 且y≠0的区域.
且y≠0的区域.
点评:本题主要考查直线与圆锥曲线的综合应用能力,具体涉及到轨迹方程的求法及直线与椭圆的相关知识,解题时要注意合理地进行等价转化.
 -y2=1,则|FF2|=2
-y2=1,则|FF2|=2 ,|PF1|+|PF2|=4>|FF2|,
,|PF1|+|PF2|=4>|FF2|,所以点P的轨迹E是以F1,F2为焦点且长轴长为4的椭圆,其方程为
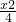 +y2=1.(3分)
+y2=1.(3分)(2)假设存在满足条件的点D(0,m),设直线a的方程为y=k(x-
 )(k≠0)
)(k≠0)代入椭圆方程得:(1+4k2)x2-8
 k2x+12k2-4=0,
k2x+12k2-4=0,设A(x1,y1),B(x2,y2),由韦达定理得:x1+x2=
 ,y1+y2=k(x1+x2-2
,y1+y2=k(x1+x2-2 )=
)=
 =(x1,y1-m),
=(x1,y1-m),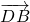 =(x2,y2-m),
=(x2,y2-m), =( x1+x2,y1+y2-2m),(6分)
=( x1+x2,y1+y2-2m),(6分)又
 =λ(1,k) (λ=x2-x1),
=λ(1,k) (λ=x2-x1),∵以DA、DB为邻边的平行四边形为菱形,∴(
 +
+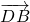 )⊥
)⊥
∴(
 +
+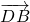 )•
)• =0,即
=0,即 +
+ -2mk=0,整理得:
-2mk=0,整理得: -2mk=0,(8分)
-2mk=0,(8分)∵k≠0,∴m=
 =
=
若k>0,则
 ≤
≤ (当且仅当k=
(当且仅当k= 时取等号),即m∈(0,
时取等号),即m∈(0, ](10分)
](10分)若k<0,则
 ≥-
≥- (当且仅当k=-
(当且仅当k=- 时取等号),即m∈[-
时取等号),即m∈[- ,0)(11分)
,0)(11分)综上,满足条件的点D存在,其活动范围是满足-
 ≤y≤
≤y≤ 且y≠0的区域.
且y≠0的区域.分析:(1)双曲线的方程可化为
 -y2=1,则|FF2|=2
-y2=1,则|FF2|=2 ,|PF1|+|PF2|=4>|FF2|,由此知点P的轨迹E是以F1,F2为焦点且长轴长为4的椭圆,并能求出其方程.
,|PF1|+|PF2|=4>|FF2|,由此知点P的轨迹E是以F1,F2为焦点且长轴长为4的椭圆,并能求出其方程.(2)假设存在满足条件的点D(0,m),设直线a的方程为y=k(x-
 ),代入椭圆方程得:(1+4k2)x2-8
),代入椭圆方程得:(1+4k2)x2-8 k2x+12k2-4=0,再由韦达定理结合分类讨论思想能够推导出满足条件的点D存在,其活动范围是满足-
k2x+12k2-4=0,再由韦达定理结合分类讨论思想能够推导出满足条件的点D存在,其活动范围是满足- ≤y≤
≤y≤ 且y≠0的区域.
且y≠0的区域.点评:本题主要考查直线与圆锥曲线的综合应用能力,具体涉及到轨迹方程的求法及直线与椭圆的相关知识,解题时要注意合理地进行等价转化.

练习册系列答案
 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目