题目内容
己知三角形ABC中,角A、B、C的对边分别为a,b,c,且A=2B,a=
b,则cosB等于 .
| 3 |
| 2 |
考点:正弦定理
专题:计算题,三角函数的求值,解三角形
分析:对A=2B两边取正弦,运用二倍角公式和正弦定理,化简计算即可得到cosB.
解答:
解:A=2B,即有sinA=sin2B=2sinBcosB,
由正弦定理可得,a=2bcosB,
由a=
b,则
b=2bcosB,
则有cosB=
.
故答案为:
.
由正弦定理可得,a=2bcosB,
由a=
| 3 |
| 2 |
| 3 |
| 2 |
则有cosB=
| 3 |
| 4 |
故答案为:
| 3 |
| 4 |
点评:本题考查正弦定理及运用,考查二倍角公式的运用,考查运算能力,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
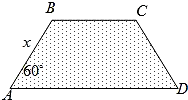 某地区要建造一条防洪堤,其横断面为等腰梯形(如图),考虑到防洪堤坚固性及石块用料等因素,设计其横断面要求面积为9
某地区要建造一条防洪堤,其横断面为等腰梯形(如图),考虑到防洪堤坚固性及石块用料等因素,设计其横断面要求面积为9| 3 |
| 3 |
| A、[3,5] |
| B、(3,5) |
| C、(2,6] |
| D、[2,6) |
 如图是输出4000以内的能被3和5整除的所有正整数的算法流程图,则在①处应填
如图是输出4000以内的能被3和5整除的所有正整数的算法流程图,则在①处应填