题目内容
(1)已知角的终边在射线y=2x(x<0)上,求sinα+cosα的值.
(2)已知角的终边上有一个点 ,且
,且 ,求sinα+cosα的值.
,求sinα+cosα的值.
解:(1)在角的终边上任取一点(-1,-2),…(2分)
则:|OP|=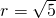 …(3分)
…(3分)
由三角函数定义知: ,
, …(5分)
…(5分)
∴ …(6分)
…(6分)
(2)因为 是α终边上的一点,
是α终边上的一点,
∴当m<0时,α是第四象限角;当m>0时,α是第二象限角.
又∵
∴cosα<0且tanα>0,或cosα>0且tanα<0
结合α是第三象限角或第四象限角,可得α是第四象限角,
∴m<0,可得r= =-
=- …(9分)
…(9分)
根据三角函数的定义,可得sinα= =-
=- ,cosα=
,cosα= =
= …(11分)
…(11分)
因此,sinα+cosα=- +
+ =
= …(12分)
…(12分)
分析:(1)在角的终边上任取一点(-1,-2),可得|OP|= ,结合三角函数的定义可得sinα和cosα的值,代入即得sinα+cosα的值.
,结合三角函数的定义可得sinα和cosα的值,代入即得sinα+cosα的值.
(2)根据角的象限进行讨论,结合 可得α是第四象限角,再算出|OP|关于m的表达式,利用三角函数的定义算出sinα和cosα的值,代入即得sinα+cosα的值.
可得α是第四象限角,再算出|OP|关于m的表达式,利用三角函数的定义算出sinα和cosα的值,代入即得sinα+cosα的值.
点评:本题给出角α终边上一点,求sinα+cosα的值.着重考查了任意角的三角函数的定义、分类讨论思想等知识,属于基础题.
则:|OP|=
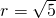 …(3分)
…(3分)由三角函数定义知:
 ,
, …(5分)
…(5分)∴
 …(6分)
…(6分)(2)因为
 是α终边上的一点,
是α终边上的一点,∴当m<0时,α是第四象限角;当m>0时,α是第二象限角.
又∵

∴cosα<0且tanα>0,或cosα>0且tanα<0
结合α是第三象限角或第四象限角,可得α是第四象限角,
∴m<0,可得r=
 =-
=- …(9分)
…(9分)根据三角函数的定义,可得sinα=
 =-
=- ,cosα=
,cosα= =
= …(11分)
…(11分)因此,sinα+cosα=-
 +
+ =
= …(12分)
…(12分)分析:(1)在角的终边上任取一点(-1,-2),可得|OP|=
 ,结合三角函数的定义可得sinα和cosα的值,代入即得sinα+cosα的值.
,结合三角函数的定义可得sinα和cosα的值,代入即得sinα+cosα的值.(2)根据角的象限进行讨论,结合
 可得α是第四象限角,再算出|OP|关于m的表达式,利用三角函数的定义算出sinα和cosα的值,代入即得sinα+cosα的值.
可得α是第四象限角,再算出|OP|关于m的表达式,利用三角函数的定义算出sinα和cosα的值,代入即得sinα+cosα的值.点评:本题给出角α终边上一点,求sinα+cosα的值.着重考查了任意角的三角函数的定义、分类讨论思想等知识,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,已知角α的终边在第二象限,且与单位圆交于点P(m,
如图,已知角α的终边在第二象限,且与单位圆交于点P(m, ,且
,且 ,求sinα+cosα的值.
,求sinα+cosα的值.