题目内容
10.设α、β、γ是三个互不重合的平面,l是直线,给出下列命题①若α⊥β,β⊥γ,则α∥γ;②若l上两点到α的距离相等,则l∥α;
③若l⊥α,l∥β,则α⊥β;④若α∥β,l∥α,l?β,则l∥β.
其中正确的命题是( )
| A. | ①② | B. | ②③ | C. | ②④ | D. | ③④ |
分析 对各个选项分别加以判断:对①和②举出反例可得它们不正确;结合空间直线与平面、平面与平面平行和垂直的判定和性质,对③和④加以论证可得它们是真命题.
解答 解:对于①,若α⊥β,β⊥γ,则α∥γ或α,γ相交,故①不正确;
对于②,若l上两个点A、B满足线段AB的中点在平面内,则A、B到α的距离相等,但l与α相交,故②不正确;
对于③,若l⊥α,l∥β,则根据面面垂直的判定定理可知α⊥β,故③正确;
对于④,若α∥β且l∥α,可得l∥β或l在β内,而条件中有l?β,所以必定l∥β,故④正确.
故选D.
点评 本题以命题真假的判断为载体,着重考查了直线与平面、平面与平面平行的判定和性质,以及直线与平面、平面与平面垂直的判定和性质等知识,属于基础题.

练习册系列答案
相关题目
20.已知角a的终边经过点P(-4,m),且$sinα=\frac{3}{5}$,则m等于( )
| A. | 3 | B. | $\frac{3}{5}$ | C. | -3 | D. | $-\frac{3}{5}$ |
1.已知函数y=Asin(ωx+ϕ)+m的最大值为4,最小值为0,最小正周期为π,直线$x=\frac{π}{6}$是其图象的一条对称轴,则下面各式中符合条件的解析式是( )
| A. | $y=4sin(2x+\frac{π}{6})$ | B. | $y=-2sin(2x+\frac{π}{6})+2$ | C. | $y=-2sin(x+\frac{π}{3})+2$ | D. | $y=2sin(2x+\frac{π}{3})+2$ |
2.在等差数列{an}中,a10=0,则有等式a1+a2+…+an=a1+a2+…+a19-n(n<19,n∈N*)成立,类比上述性质,相应地在等比数列{bn}中,若b9=1,则成立的等式是( )
| A. | b1b2…bn=b1b2…b17-n (n<17,n∈N*) | |
| B. | b1b2…bn=b1b2…b18-n(n<18,n∈N*) | |
| C. | b1+b2+…+bn=b1+b2+…+b17-n(n<17,n∈N*) | |
| D. | b1+b2+…+bn=b1+b2-1+…+b18-n(n<18,n∈N*) |
19.函数f(x)的定义域为D,对给定的正数k,若存在闭区间[a,b]⊆D,使得函数f(x)满足:①f(x)在[a,b]内是单调函数;②f(x)在[a,b]上的值域为[ka,kb],则称区间[a,b]为y=f(x)的k级“理想区间”.下列结论错误的是( )
| A. | 函数f(x)=x2(x∈R)存在1级“理想区间” | |
| B. | 函数f(x)=ex(x∈R)不存在2级“理想区间” | |
| C. | 函数f(x)=$\frac{4x}{{x}^{2}+1}$(x≥0)存在3级“理想区间” | |
| D. | 函数f(x)=tanx,x∈(-$\frac{π}{2}$,$\frac{π}{2}$)不存在4级“理想区间” |
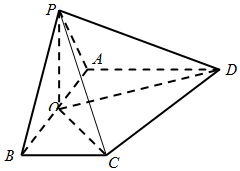 如图,已知在四棱锥P-ABCD中,O为AB中点,平面POC⊥平面ABCD,AD∥BC,AB⊥BC,PA=PB=BC=AB=2,AD=3
如图,已知在四棱锥P-ABCD中,O为AB中点,平面POC⊥平面ABCD,AD∥BC,AB⊥BC,PA=PB=BC=AB=2,AD=3