题目内容
已知数列 的前
的前 项和为
项和为 ,且
,且 ,
,
 .
.
(1)求 的值;
的值;
(2)猜想 的通项公式,并用数学归纳法证明.
的通项公式,并用数学归纳法证明.
 的前
的前 项和为
项和为 ,且
,且 ,
,
 .
.(1)求
 的值;
的值;(2)猜想
 的通项公式,并用数学归纳法证明.
的通项公式,并用数学归纳法证明.(1)
 (2)通项为
(2)通项为 证明:①当
证明:①当 时,由条件知等式成立,②假设当
时,由条件知等式成立,②假设当 (
( 且
且 )等式成立,即:
)等式成立,即:
那么当 时,
时, ,
,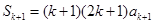 ,由
,由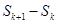 得
得
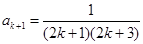 由①②可知,命题对一切
由①②可知,命题对一切 都成立
都成立

 (2)通项为
(2)通项为 证明:①当
证明:①当 时,由条件知等式成立,②假设当
时,由条件知等式成立,②假设当 (
( 且
且 )等式成立,即:
)等式成立,即:
那么当
 时,
时, ,
,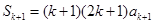 ,由
,由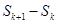 得
得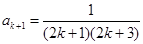 由①②可知,命题对一切
由①②可知,命题对一切 都成立
都成立试题分析:⑴

 ,且
,且
 当
当 时,
时, ,解得:
,解得: ;
;当
 时,
时, ,解得:
,解得:
⑵由⑴可以猜想
 的通项为
的通项为
用数学归纳法证明如下:
①当
 时,由条件知等式成立;
时,由条件知等式成立;②假设当
 (
( 且
且 )等式成立,即:
)等式成立,即:
那么当
 时,由条件
时,由条件 有:
有: ;
; 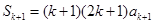

 ,即
,即 ,
, 
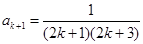 ,即:当
,即:当 时等式也成立.
时等式也成立.由①②可知,命题对一切
 都成立.
都成立.点评:已知条件是关于
 的关系式,此关系式经常用到
的关系式,此关系式经常用到
有关于正整数的命题常用数学归纳法证明,其主要步骤:第一步,n取最小的正整数时命题成立,第二步,假设
 时命题成立,借此来证明
时命题成立,借此来证明 时命题成立
时命题成立
练习册系列答案
相关题目
 中,各项均为正数,且
中,各项均为正数,且 则数列
则数列 ;前n项和
;前n项和 = .
= . 中,
中, ,
, .
. ,求证数列
,求证数列 是等比数列;
是等比数列; 的前
的前 项和
项和
 ,则此数列的通项公式为 .
,则此数列的通项公式为 . }满足a
}满足a =2a
=2a +a
+a ,且a
,且a +a
+a =2a
=2a +4,其中n∈N
+4,其中n∈N .
. ,求数列{b
,求数列{b +
+ +…+
+…+ >
> (n≥2).
(n≥2). (
( )个平面最多将空间分成 ( )
)个平面最多将空间分成 ( ) 部分
部分 部分
部分 部分
部分 部分
部分 ,n∈N﹡,数列{bn}满足an=4log2bn+3,n∈N﹡。
,n∈N﹡,数列{bn}满足an=4log2bn+3,n∈N﹡。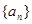 是等差数列,
是等差数列,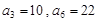 ,数列
,数列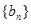 的前n项和是
的前n项和是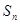 ,且
,且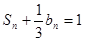 .
.