题目内容
一个平面将空间分成两部分,两个平面将空间最多分成四部分,三个平面最多将空间分成八部分,…,由此猜测 (
( )个平面最多将空间分成 ( )
)个平面最多将空间分成 ( )
 (
( )个平面最多将空间分成 ( )
)个平面最多将空间分成 ( )A. 部分 部分 | B. 部分 部分 | C. 部分 部分 | D. 部分 部分 |
D
试题分析:设k个平面最多将空间分成
 部分,增加一个平面与原来的k个平面相交出现k条交线,这k条交线将第k个平面分割成n个部分,从而增加k+1个区域,可得递推关系式
部分,增加一个平面与原来的k个平面相交出现k条交线,这k条交线将第k个平面分割成n个部分,从而增加k+1个区域,可得递推关系式 ,即
,即 ,
, 累和得
累和得 ,即
,即
点评:当分成的空间部分最多时,增加的平面与原来各平面都相交,据此找到第k+1个平面与前k个平面的递推关系,本题有一定的难度

练习册系列答案
相关题目
 是公差不为0的等差数列
是公差不为0的等差数列 的前
的前 项和,且
项和,且 成等比数列。
成等比数列。 ,求
,求 ,
, 是数列
是数列 的前
的前 对所有
对所有 都成立的最小正整数
都成立的最小正整数 。
。 的前
的前 项和为
项和为 ,
, ,
, ,,则
,,则 .
.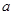
 },(n∈N
},(n∈N )是等差数列,则有数列b
)是等差数列,则有数列b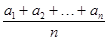 (n∈N
(n∈N 的前
的前 项和为
项和为 ,且
,且 ,
,
 .
. 的值;
的值; 满足
满足 (
( ).
). 可以生成的数列
可以生成的数列 ”是“数列
”是“数列 为单调递增数列,则
为单调递增数列,则 ;
; ,其中
,其中 ,则
,则 一定存在;
一定存在; 的通项公式为
的通项公式为 ,则数列
,则数列 的前10项的和为( )
的前10项的和为( ) 满足
满足 ,若
,若 ,则
,则 ( )
( )




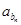 <0.001成立的最小的n值.
<0.001成立的最小的n值.