题目内容
动点A(x,y)在单位圆x2+y2=1上绕圆心顺时针方向匀速旋转,12秒旋转一周.已知t=0时点A(
,
),则当0≤t≤12时,动点A的纵坐标y关于t的函数y=f(t)的单调增区间是( )
| 1 |
| 2 |
| ||
| 2 |
| A、[0,5] |
| B、[5,11] |
| C、[11,12] |
| D、[0,5]和[11,12] |
考点:正弦函数的单调性
专题:三角函数的图像与性质
分析:首先,设y关于t的函数:y=sin(-ωt+θ),然后确定ω=
=
,θ=
,从而,得到函数解析式y=sin(-
t+
)=-sin(
t-
),最后,借助于三角函数的单调性进行求解.
| 2π |
| 12 |
| π |
| 6 |
| π |
| 3 |
| π |
| 6 |
| π |
| 3 |
| π |
| 6 |
| π |
| 3 |
解答:
解:设y关于t的函数:y=sin(-ωt+θ)
∵12秒旋转一周,
∴T=
=12,
∴ω=
=
,
∵当t=0时,点A(
,
),
将该点代人,得到θ=
,
∴y=sin(-
t+
)=-sin(
t-
),
令
+2kπ≤
t-
≤
+2kπ,k∈Z,
∴5+2k≤t≤11+2k,
∵0≤t≤12,
则当0≤t≤12时,动点A的纵坐标y关于t(单位:秒)的函数的单调递增区间是[5,11],
故选:B.
∵12秒旋转一周,
∴T=
| 2π |
| ω |
∴ω=
| 2π |
| 12 |
| π |
| 6 |
∵当t=0时,点A(
| 1 |
| 2 |
| ||
| 2 |
将该点代人,得到θ=
| π |
| 3 |
∴y=sin(-
| π |
| 6 |
| π |
| 3 |
| π |
| 6 |
| π |
| 3 |
令
| π |
| 2 |
| π |
| 6 |
| π |
| 3 |
| 3π |
| 2 |
∴5+2k≤t≤11+2k,
∵0≤t≤12,
则当0≤t≤12时,动点A的纵坐标y关于t(单位:秒)的函数的单调递增区间是[5,11],
故选:B.
点评:本题考查函数的单调性及单调区间,体现了转化的数学思想.属于中档题.

练习册系列答案
 天天练口算系列答案
天天练口算系列答案
相关题目
设x,y∈R,a>0,且|x|+|y|≤a,2x+y+1最大值小于2,则实数a的取值范围为( )
| A、(0,1) | ||
B、(0,
| ||
C、[
| ||
| D、(0,1] |
已知x与y之间的一组数据如表所示,则x与y的回归直线必过点( )
| x | 0 | 1 | 2 | 3 |
| y | 1 | 3 | 5 | 7 |
| A、(2,2) |
| B、(1.5,0) |
| C、(1,2) |
| D、(1.5,4) |
在区间[0,π]内随机取两个数分别记为a、b,则使得函数f(x)=x2+2ax-b2+π有零点的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
执行如图所示的程序框图,则输出的n为( )


| A、4 | B、5 | C、6 | D、7 |
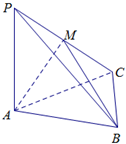 如图,底面是正三角形的三棱锥P-ABC中,PA⊥底面ABC,M为PC中点,且PA=AB,其中下列四个命题:
如图,底面是正三角形的三棱锥P-ABC中,PA⊥底面ABC,M为PC中点,且PA=AB,其中下列四个命题: