题目内容
选修4-4:(坐标系与参数方程)将参数方程
|
分析:方法一:根据(t+
)2-(t-
)2=4,由参数方程表示出t+
及t-
,代入化简可得关于x与y的普通方程;
方法二:由参数方程两方程相加表示出t,两方程相减表示出
,得到的两等式左右两边相乘,根据互为倒数的两数积为1即可消去参数t,得到关于x与y的普通方程.
| 1 |
| t |
| 1 |
| t |
| 1 |
| t |
| 1 |
| t |
方法二:由参数方程两方程相加表示出t,两方程相减表示出
| 1 |
| t |
解答:解:(方法一)
因为(t+
)2-(t-
)2=4,(5分)
所以(
)2-(
)2=4,(8分)
化简得普通方程为
-
=1.(10分)
(方法二)
因为
,所以t=
,
=
,(5分)
相乘得
=1,(8分)
化简得普通方程为
-
=1.(10分)
因为(t+
| 1 |
| t |
| 1 |
| t |
所以(
| x |
| 2 |
| y |
| 4 |
化简得普通方程为
| x2 |
| 16 |
| y2 |
| 64 |
(方法二)
因为
|
| 2x+y |
| 8 |
| 1 |
| t |
| 2x-y |
| 8 |
相乘得
| (2x+y)(2x-y) |
| 64 |
化简得普通方程为
| x2 |
| 16 |
| y2 |
| 64 |
点评:此题考查了参数方程化成普通方程的方法,不管采用什么方法,其目的都是消去参数t,得到关于x与y的普通方程,消去参数t的过程体现了转化及消元的数学思想.

练习册系列答案
相关题目
 【选做题】在A,B,C,D四小题中只能选做2题,每小题10分,共计20分.请在答题卡指定区域内作答.解答应写出文字说明、证明过程或演算步骤.
【选做题】在A,B,C,D四小题中只能选做2题,每小题10分,共计20分.请在答题卡指定区域内作答.解答应写出文字说明、证明过程或演算步骤.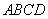 是边长为
是边长为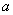 的正方形,以
的正方形,以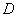 为圆心,
为圆心,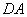 为半径的圆弧与以
为半径的圆弧与以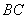 为直径的
为直径的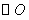 交于点
交于点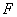 ,延长
,延长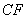 交
交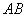 于
于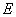 .(1)求证:
.(1)求证: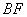 的长.
的长.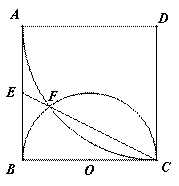
 ,若矩阵
,若矩阵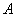 属于特征值3的一个特征向量为
属于特征值3的一个特征向量为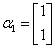 ,属于特征值-1的一个特征向量为
,属于特征值-1的一个特征向量为 ,求矩阵
,求矩阵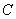 的极坐标方程为
的极坐标方程为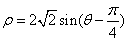 ,以极点为原点,极轴为
,以极点为原点,极轴为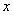 轴的正半轴建立平面直角坐标系,直线
轴的正半轴建立平面直角坐标系,直线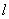 的参数方程为
的参数方程为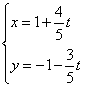 (
(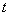 为参数),求直线
为参数),求直线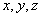 满足
满足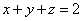 ,求
,求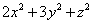 的最小值;
的最小值;