Question

【题目】以椭圆的中心O为圆心，以为半径的圆称为该椭圆的“伴随”．已知椭圆的离心率为，且过点．

（1）求椭圆C及其“伴随”的方程；

（2）过点作“伴随”的切线l交椭圆C于A，B两点，记为坐标原点）的面积为，将表示为m的函数，并求的最大值．

Answer 1

【答案】（1）,；（2），，的最大值为1．

【解析】

（1）由椭圆C的离心率，结合的关系，得到，设出椭圆方程，代入点，即可得到椭圆方程和“伴随”的方程；

（2）设切线的方程为，联立椭圆方程，消去y得到x的二次方程，运用韦达定理和弦长公式，即可得到AB的长，由l与圆相切，得到的关系式，求出 的面积，运用基本不等式，即可得到最大值．

（1）椭圆的离心率为，可得，即

又由，可得，

设椭圆C的方程为，

因为椭圆C过点，代入可得，

解得，所以椭圆C的标准方程为，

又由，即“伴随圆”是以原点为圆心，半径为1的圆，

所以椭圆C的“伴随”方程为．

（2）由题意知，，

易知切线的斜率存在，设切线的方程为，

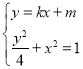由得，

设A，B两点的坐标分别为（x1，y1），（x2，y2），

则，．

又由l与圆x2+y2=1相切，所以，k2=m2-1．

所以=，

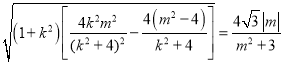则，，

可得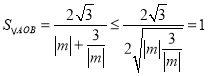（当且仅当时取等号），

所以当时，S△AOB的最大值为1．