题目内容
【题目】已知椭圆
的左，右焦点分别为
，
，
，M是椭圆E上的一个动点，且
的面积的最大值为
.
（1）求椭圆E的标准方程，
（2）若
，
，四边形ABCD内接于椭圆E，
，记直线AD，BC的斜率分别为
，
，求证:
为定值.
【答案】（1）
（2）证明见解析
【解析】
（1）设椭圆E的半焦距为c，由题意可知，当M为椭圆E的上顶点或下顶点时，
的面积取得最大值
，求出
，即可得答案；
（2）根据题意可知
，
，因为
，所以可设直线CD的方程为
，将直线代入曲线的方程，利用韦达定理得到
的关系，再代入斜率公式可证得
为定值.
（1）设椭圆E的半焦距为c，由题意可知，
当M为椭圆E的上顶点或下顶点时，的面积取得最大值.
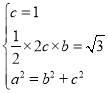所以
，所以
，
，
故椭圆E的标准方程为.
（2）根据题意可知，，因为，
所以可设直线CD的方程为.
由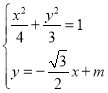
，消去y可得
，
所以
，即
.
直线AD的斜率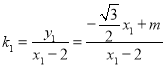
，
直线BC的斜率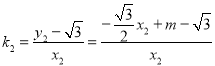
，
所以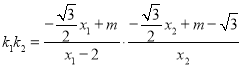
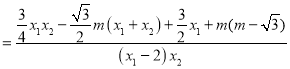
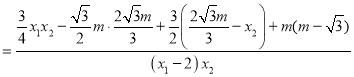
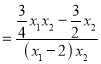
，故为定值.
练习册系列答案
相关题目
