题目内容
方程x3=2-x的实根的个数是（ ）
| A、0 | B、1 | C、2 | D、3 |
考点：根的存在性及根的个数判断
专题：数形结合,函数的性质及应用
分析：分析：方程x3=2-x的实根即为函数y=x3与函数y=2-x图象交点的横坐标，因此，根的个数即为两函数图象交点的个数，因此只需做出上述两函数的图象观查即可获解．
解答：
解：由题意知：方程x3=2-x的实根即为函数y=x3与函数y=2-x图象交点的横坐标，∴原方程实根的个数即为函数y=x3与函数y=2-x图象交点的个数．
在同一坐标系中画出两函数图象如下：
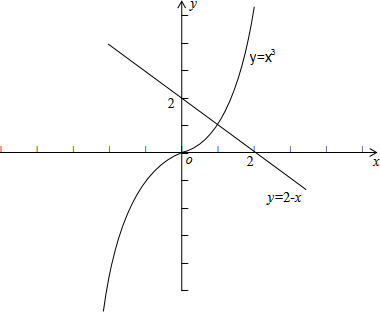
从图象可以看出，两函数图象只有一个公共点，所以原方程只有一个实数根．
故选：B．
在同一坐标系中画出两函数图象如下：
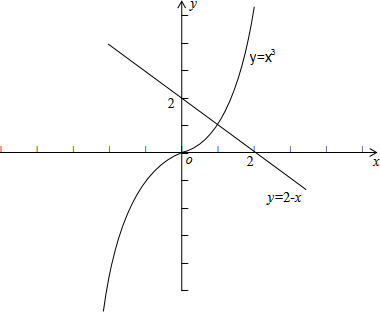
从图象可以看出，两函数图象只有一个公共点，所以原方程只有一个实数根．
故选：B．
点评：本题考查了函数的零点、方程的根、图象间交点的横坐标三者的关系，三者之间可以相互转化，互为解题方法．本题重点考查了数形结合的思想方法．
练习册系列答案
相关题目
要得到y=
cos2x+sinxcosx的图象，只需把y=sin2x的图象上所有点（ ）
| 3 |
A、向左平移
| ||||||
B、向左平移
| ||||||
C、向右平移
| ||||||
D、向右平移
|
已知直线y=x与圆：（x-1）2+y2=1相交于点A，B，则弦|AB|的长为（ ）
| A、1 | ||||
B、
| ||||
C、
| ||||
D、
|
下列函数中，在其定义域内既是奇函数又是减函数的是（ ）
| A、y=|x| | ||
| B、y=-x3 | ||
| C、y=0.9x | ||
D、y=log
|
下列从A到B的对应法则f是映射的是（ ）
| A、A=R，B=R+，f：取绝对值 |
| B、A=R+，B=R，f：开平方 |
| C、A=R+，B=R，f：取对数 |
| D、A=Q，B={偶数}，f：乘2 |
命题“?x0∈R，2x0≤0”的否定是（ ）
| A、?x0∈R，2x0＞0 |
| B、?x0∉R，2x0≤0 |
| C、?x∈R，2x＞0 |
| D、?x∈R，2x≤0 |
（文科）如图，在棱长为4的正方体ABCD-A1B1C1D1中，P、Q分别是棱A1D1和AD的中点，R为PB的中点．