题目内容
已知函数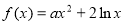 (
(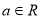 )
)
(1)若曲线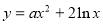 在
在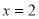 处的切线
处的切线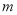 与直线
与直线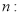
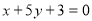 垂直,试确定
垂直,试确定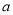 的值;并求出该曲线在点
的值;并求出该曲线在点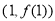 处的切线方程.
处的切线方程.
(2)若函数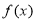 在
在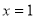 时,取得极值,试确定
时,取得极值,试确定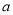 的值,并求出
的值,并求出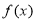 的单调区间;
的单调区间;
(1)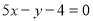 ;(2)
;(2)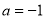 ,增区间为:
,增区间为: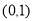 ,减区间为:
,减区间为: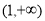 .
.
【解析】
试题分析:(1)求导,利用导数的几何意义写出切线方程,利用两直线垂直求出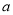 值,代入即可切线方程;(2)求导,先利用存在极值求得
值,代入即可切线方程;(2)求导,先利用存在极值求得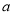 值,再利用导函数的正负求出函数的单调区间.
值,再利用导函数的正负求出函数的单调区间.
解题思路:利用导数的几何意义求曲线的切线方程的一般步骤:第一步,求导;第二步,求斜率;第三步,写出切线方程的点斜式方程,化成一般式方程.
试题解析:(1)由已知直线n的斜率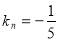
则与之垂直的切线m的斜率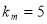 1分
1分
求导,得: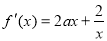 2分
2分
令: 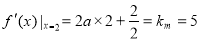 3分
3分
解得,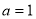 4分
4分
∴此时,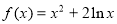 ,把x=1代入,
,把x=1代入,
得: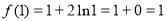 ,则切点为(1,1) 5分
,则切点为(1,1) 5分
写出切线方程: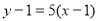 即
即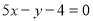 6分
6分
(2)求导,得: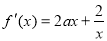 7分
7分
由题意(在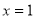 时,取得极值),即
时,取得极值),即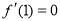
∴ 8分
8分
解出: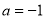 9分
9分
∴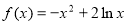 ,
,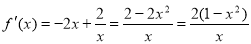
由于,函数的定义域显然为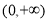 ,即x>0 10分
,即x>0 10分
∴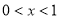 时,
时,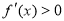 ,则原函数为增函数,
,则原函数为增函数,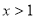 时,
时,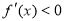 ,则原函数为减函数, 11分
,则原函数为减函数, 11分
∴原函数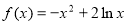 的增区间为:
的增区间为: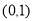
原函数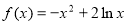 的减区间为:
的减区间为: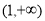
考点:1.导数的几何意义;(2)函数的极值;3.函数的单调区间.

练习册系列答案
相关题目
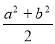 ”的 ( )
”的 ( ) 的右焦点与抛物线
的右焦点与抛物线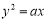 的焦点重合,则该抛物线的准线被双曲线所截的线段长度为( )
的焦点重合,则该抛物线的准线被双曲线所截的线段长度为( )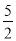 D.
D.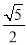
 的近似解在区间
的近似解在区间 ,则
,则 .
. 的值域为 .
的值域为 . ,则导数
,则导数 .
. 的图像如左图所示,那么函数
的图像如左图所示,那么函数 的图像最有可能的是
的图像最有可能的是 
 ,一个等比中项是
,一个等比中项是 ,且
,且 则双曲线
则双曲线 的离子心率e等于___________;
的离子心率e等于___________;