题目内容
已知函数f(x)=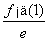 ·ex-f(0)·x+
·ex-f(0)·x+ x2(e是自然对数的底数).
x2(e是自然对数的底数).
(1)求函数f(x)的解析式和单调区间;
(2)若函数g(x)= x2+a与函数f(x)的图像在区间[-1,2]上恰有两个不同的交点,求实数a的取值范围.
x2+a与函数f(x)的图像在区间[-1,2]上恰有两个不同的交点,求实数a的取值范围.
解:(1)由已知得f′(x)=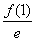 ex-f(0)+x,
ex-f(0)+x,
令x=1,得f′(1)=f′(1)-f(0)+1,
即f(0)=1.又f(0)=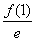 ,所以f′(1)=e.
,所以f′(1)=e.
从而f(x)=ex-x+ x2.
x2.
显然f′(x)=ex-1+x在R上单调递增且
f′(0)=0,故当x∈(-∞,0)时,f′(x)<0;
当x∈(0,+∞)时,f′(x)>0.
∴f(x)的单调递减区间是(-∞,0),
单调递增区间是(0,+∞).
(2)由f(x)=g(x)得a=ex-x.
令h(x)=ex-x,则h′(x)=ex-1.
由h′(x)=0得x=0.
所以当x∈(-1,0)时,h′(x)<0;
当x∈(0,2)时,h′(x)>0.
∴h(x)在(-1,0)上单调递减,
在(0,2)上单调递增.
又h(0)=1,h(-1)=1+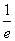 ,h(2)=e2-2
,h(2)=e2-2
且h(-1)<h(2).
∴两个图像恰有两个不同的交点时,
实数a的取值范围是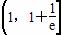 .
.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
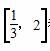 都有|f(x)|≤1成立,试求a的取值范围.
都有|f(x)|≤1成立,试求a的取值范围.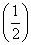 ,c=f(3),则( )
,c=f(3),则( )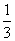 x3+
x3+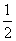 x2+2ax.
x2+2ax.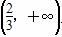 上存在单调递增区间,求a的取值范围;
上存在单调递增区间,求a的取值范围;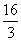 ,求f(x)在该区间上的最大值.
,求f(x)在该区间上的最大值.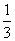 x3-
x3- x2-40x(x>0),为使耗电量最小,则速度应定为________.
x2-40x(x>0),为使耗电量最小,则速度应定为________. 弧长到达Q点,则Q点的坐标为( )
弧长到达Q点,则Q点的坐标为( )
 的角α的集合为________.
的角α的集合为________.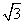 cos(2x+φ)+sin(2x+φ)
cos(2x+φ)+sin(2x+φ) 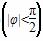 ,且其图像关于直线x=0对称,则( )
,且其图像关于直线x=0对称,则( ) 上为增函数
上为增函数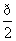 ,且在
,且在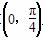 上为增函数
上为增函数 的图象向____平移 ____个单位长度就可得到函数y=sin2x的图象。
的图象向____平移 ____个单位长度就可得到函数y=sin2x的图象。