题目内容
已知θ为第四象限角,且cosθ=
,求sin(2θ+
)的值.
| 3 |
| 5 |
| π |
| 3 |
分析:由题意,θ为第四象限角,且cosθ=
,可先由同角三角函数的基本关系求出θ的正弦,再由二倍角公式求出2θ的正弦与余弦,然后由正弦的和角公式求出sin(2θ+
)的值即可得到答案
| 3 |
| 5 |
| π |
| 3 |
解答:解:由θ为第四象限角,且cosθ=
得sinθ=-
(2分)
又sin2θ=2sinθcosθ=2•(-
)•
=-
(2分)
∴cos2θ=cos2θ-sin2θ=(
)2-(-
)2=-
(2分)
∴sin(2θ+
)=sin2θ•cos
+cos2θ•sin
=(-
)•
+(-
)•
=
(2分)
| 3 |
| 5 |
| 4 |
| 5 |
又sin2θ=2sinθcosθ=2•(-
| 4 |
| 5 |
| 3 |
| 5 |
| 24 |
| 25 |
∴cos2θ=cos2θ-sin2θ=(
| 3 |
| 5 |
| 4 |
| 5 |
| 7 |
| 25 |
∴sin(2θ+
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
| 24 |
| 25 |
| 1 |
| 2 |
| 7 |
| 25 |
| ||
| 2 |
-24-7
| ||
| 50 |
点评:本题考点是三角函数的恒等变换及化简求值,考查了同角三角函数的基本关系,二倍角的正弦与余弦,正弦的和角公式,解题的关键是熟练掌握三角函数的公式,利用公式求值,三角函数公式较多,变形灵活,做题时要注意总结规律,找到最佳的变形方法进行求值

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
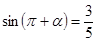 且
且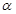 为第四象限角,则
为第四象限角,则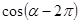 的值是( )
的值是( )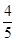 B.
B.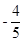 C.
C.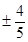 D.
D.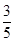
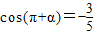 且α为第四象限角,则sin(-2π+α)= .
且α为第四象限角,则sin(-2π+α)= . ,则tanα= .
,则tanα= .