题目内容
1. 在平行六面体ABCD-A'B'C'D'中,AB=4,AD=6,AA'=8,$∠BAD=\frac{π}{2}$,$∠DAA'=∠BAA'=\frac{π}{3}$,P是CC1的中点.则AP=6$\sqrt{3}$.
在平行六面体ABCD-A'B'C'D'中,AB=4,AD=6,AA'=8,$∠BAD=\frac{π}{2}$,$∠DAA'=∠BAA'=\frac{π}{3}$,P是CC1的中点.则AP=6$\sqrt{3}$.
分析 由题意可知$\overrightarrow{AP}$=$\overrightarrow{AB}+\overrightarrow{AD}+\frac{1}{2}\overrightarrow{AA′}$,两边平方即可求出${\overrightarrow{AP}}^{2}$,从而得出AP的值.
解答 解:由题意可知$\overrightarrow{AP}$=$\overrightarrow{AB}+\overrightarrow{AD}+\frac{1}{2}\overrightarrow{AA′}$,
又${\overrightarrow{AB}}^{2}$=16,${\overrightarrow{AD}}^{2}$=36,${\overrightarrow{AA′}}^{2}$=64,
$\overrightarrow{AB}•\overrightarrow{AD}$=4×6×cos$\frac{π}{2}$=0,$\overrightarrow{AB}•\overrightarrow{AA′}$=4×8×cos$\frac{π}{3}$=16,$\overrightarrow{AD}•\overrightarrow{AA′}$=6×8×cos$\frac{π}{3}$=24,
∴${\overrightarrow{AP}}^{2}$=${\overrightarrow{AB}}^{2}$+${\overrightarrow{AD}}^{2}$+$\frac{1}{4}$${\overrightarrow{AA′}}^{2}$+2$\overrightarrow{AB}•\overrightarrow{AD}$+$\overrightarrow{AB}•\overrightarrow{AA′}$+$\overrightarrow{AD}•\overrightarrow{AA′}$=16+36+16+0+16+24=108,
∴AP=|$\overrightarrow{AP}$|=$\sqrt{108}$=6$\sqrt{3}$.
故答案为:6$\sqrt{3}$.
点评 本题考查了空间向量的应用与空间距离的计算,属于中档题.

| A. | 9 | B. | 4 | C. | $\frac{9}{2}$ | D. | $\frac{3}{2}$ |
| A. | $\sqrt{3}$ | B. | $\frac{{\sqrt{3}}}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{{\sqrt{3}}}{2}$ |
| A. | $\frac{63}{125}$ | B. | $\frac{62}{125}$ | C. | $\frac{63}{250}$ | D. | $\frac{31}{125}$ |
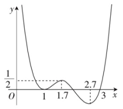 函数f(x)的图象如图所示,则f(x)的极大值点为( )
函数f(x)的图象如图所示,则f(x)的极大值点为( )| A. | $\frac{1}{2}$ | B. | 1 | C. | 1.7 | D. | 2.7 |
 如图,正方体A1B1C1D1-ABCD中,E、F是对角线B1D1、A1D的中点,
如图,正方体A1B1C1D1-ABCD中,E、F是对角线B1D1、A1D的中点, 绘制一块菜地的平面图形使用斜二测得画法得到的直观图是直角梯形ABCD,如图所示,∠ABC=45°,DC⊥AD,DC⊥BC,AD=DC=2,BC=4,则这块菜地的面积为12$\sqrt{2}$.
绘制一块菜地的平面图形使用斜二测得画法得到的直观图是直角梯形ABCD,如图所示,∠ABC=45°,DC⊥AD,DC⊥BC,AD=DC=2,BC=4,则这块菜地的面积为12$\sqrt{2}$.