题目内容
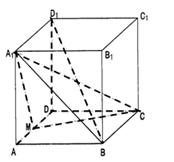
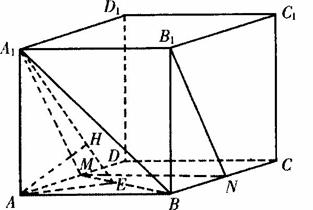
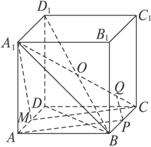
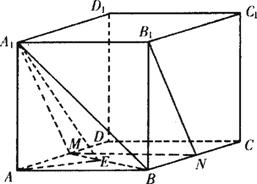
已知如图,在长方体ABCD-A1B1C1D1中,AB=2BC=2AA1=2,点E在棱AB上移动,点F为CD1的中点.(1)求三棱锥D1-ADC的体积;
(2)当AE为多长时,EF∥平面DA1D1?并证明你的结论;
(3)求证:A1D⊥D1E.
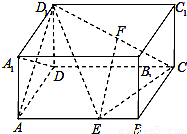
【答案】分析:(1)利用长方体的性质可得DD1⊥ABCD,S△ADC,及三棱锥的体积计算公式即可得出;
(2)当AE=1时,即为相等AB的中点时,EF∥平面DA1D1. 取CD的中点G,连接FG,EG,利用三角形的中位线定理及平行四边形的性质即可得出FG∥D1D,EG∥AD,再利用线面平行的判定定理即可得出;
(3)由正方形ADD1A1得A1D⊥AD1,又AB⊥A1D即可证明A1D⊥对角面ABC1D1.
解答:解:(1)因为ABCD-A1B1C1D1为长方体,
所以DD1⊥ABCD, ,
,
所以 =
= .
.
(2)当AE=1时,EF∥平面DA1D1.
证明如下:
取CD的中点G,连接FG,EG,则FG∥D1D,EG∥AD,
又因为EG∩FG=G,所以平面EFG∥平面DA1D1,
因为EF?平面EFG,所以EF∥平面DA1D1.
(3)因为ABCD-A1B1C1D1为长方体,所以AB⊥ADD1A1,
又因为A1D?平面ADD1A1,所以AB⊥A1D.
因为BC=AA1,所以四边形A1ADD1为正方形,所以A1D⊥AD1.
又因为AB∩AD1=A,所以A1D⊥平面ABC1D1;
又因为D1E?平面ABC1D1,所以A1D⊥D1E.
点评:本题综合考查了长方体的性质、线面垂直的判定与性质定理、线面与面面平行的判定与性质定理、三角形的中位线定理、平行四边形及正方形的性质等基础知识,考查了空间想象能力、推理能力和计算能力.
(2)当AE=1时,即为相等AB的中点时,EF∥平面DA1D1. 取CD的中点G,连接FG,EG,利用三角形的中位线定理及平行四边形的性质即可得出FG∥D1D,EG∥AD,再利用线面平行的判定定理即可得出;
(3)由正方形ADD1A1得A1D⊥AD1,又AB⊥A1D即可证明A1D⊥对角面ABC1D1.
解答:解:(1)因为ABCD-A1B1C1D1为长方体,
所以DD1⊥ABCD,
 ,
,所以
 =
= .
. (2)当AE=1时,EF∥平面DA1D1.
证明如下:
取CD的中点G,连接FG,EG,则FG∥D1D,EG∥AD,
又因为EG∩FG=G,所以平面EFG∥平面DA1D1,
因为EF?平面EFG,所以EF∥平面DA1D1.
(3)因为ABCD-A1B1C1D1为长方体,所以AB⊥ADD1A1,
又因为A1D?平面ADD1A1,所以AB⊥A1D.
因为BC=AA1,所以四边形A1ADD1为正方形,所以A1D⊥AD1.
又因为AB∩AD1=A,所以A1D⊥平面ABC1D1;
又因为D1E?平面ABC1D1,所以A1D⊥D1E.
点评:本题综合考查了长方体的性质、线面垂直的判定与性质定理、线面与面面平行的判定与性质定理、三角形的中位线定理、平行四边形及正方形的性质等基础知识,考查了空间想象能力、推理能力和计算能力.

练习册系列答案
 一本好题口算题卡系列答案
一本好题口算题卡系列答案
相关题目
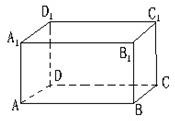 已知如图:长方体ABCD-A1B1C1D1中,交于顶点A的三条棱长别为AD=3,AA1=4,AB=5.一天,小强观察到在A处有一只蚂蚁,发现顶点C1处有食物,于是它沿着长方体的表面爬行去获取食物,则蚂蚁爬行的最短路程是( )
已知如图:长方体ABCD-A1B1C1D1中,交于顶点A的三条棱长别为AD=3,AA1=4,AB=5.一天,小强观察到在A处有一只蚂蚁,发现顶点C1处有食物,于是它沿着长方体的表面爬行去获取食物,则蚂蚁爬行的最短路程是( )