题目内容
写出函数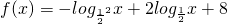 的单调区间.
的单调区间.
解:设μ= ,x>0.
,x>0.
则原函数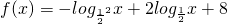 是函数y=-μ2+2μ+8,μ=
是函数y=-μ2+2μ+8,μ= 的复合函数,
的复合函数,
因μ= 在(0,+∞)上是减函数,
在(0,+∞)上是减函数,
∵函数y=-μ2+2μ+8的单调增区间(-∞,1],单调减区间[1,+∞),
∴根据复合函数的单调性,得
①函数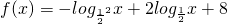 的单调减区间是函数y=-μ2+2μ+8的单调增区间,
的单调减区间是函数y=-μ2+2μ+8的单调增区间,
由μ≤1得: ≤1,?x≥
≤1,?x≥ ;
;
②函数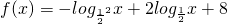 的单调增区间是函数y=-μ2+2μ+8的单调减区间,
的单调增区间是函数y=-μ2+2μ+8的单调减区间,
由μ≥1得: ≥1,?0≤x≤
≥1,?0≤x≤ ;
;
故函数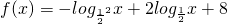 的单调区间是:[
的单调区间是:[ ,+∝),(0,
,+∝),(0, ].
].
分析:将原函数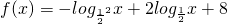 是函数:y=-μ2+2μ+8,μ=
是函数:y=-μ2+2μ+8,μ= 的复合函数,利用对数函数与二次函数的单调性来研究即可.注意对数的真数必须大于0.
的复合函数,利用对数函数与二次函数的单调性来研究即可.注意对数的真数必须大于0.
点评:本题考查复合函数的单调性,指数函数的单调性,二次函数的单调性,是基础题. 复合函数的单调性一般是看函数包含的两个函数的单调性(1)如果两个都是增的,那么函数就是增函数(2)一个是减一个是增,那就是减函数(3)两个都是减,那就是增函数.
 ,x>0.
,x>0.则原函数
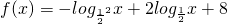 是函数y=-μ2+2μ+8,μ=
是函数y=-μ2+2μ+8,μ= 的复合函数,
的复合函数,因μ=
 在(0,+∞)上是减函数,
在(0,+∞)上是减函数,∵函数y=-μ2+2μ+8的单调增区间(-∞,1],单调减区间[1,+∞),
∴根据复合函数的单调性,得
①函数
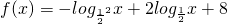 的单调减区间是函数y=-μ2+2μ+8的单调增区间,
的单调减区间是函数y=-μ2+2μ+8的单调增区间,由μ≤1得:
 ≤1,?x≥
≤1,?x≥ ;
;②函数
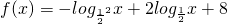 的单调增区间是函数y=-μ2+2μ+8的单调减区间,
的单调增区间是函数y=-μ2+2μ+8的单调减区间,由μ≥1得:
 ≥1,?0≤x≤
≥1,?0≤x≤ ;
;故函数
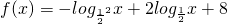 的单调区间是:[
的单调区间是:[ ,+∝),(0,
,+∝),(0, ].
].分析:将原函数
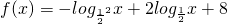 是函数:y=-μ2+2μ+8,μ=
是函数:y=-μ2+2μ+8,μ= 的复合函数,利用对数函数与二次函数的单调性来研究即可.注意对数的真数必须大于0.
的复合函数,利用对数函数与二次函数的单调性来研究即可.注意对数的真数必须大于0.点评:本题考查复合函数的单调性,指数函数的单调性,二次函数的单调性,是基础题. 复合函数的单调性一般是看函数包含的两个函数的单调性(1)如果两个都是增的,那么函数就是增函数(2)一个是减一个是增,那就是减函数(3)两个都是减,那就是增函数.

练习册系列答案
相关题目