题目内容
已知椭圆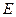 :
: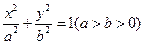 的离心率为
的离心率为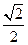 ,且过点
,且过点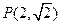 ,设椭圆的右准线
,设椭圆的右准线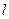 与
与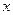 轴的交点为
轴的交点为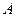 ,椭圆的上顶点为
,椭圆的上顶点为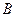 ,直线
,直线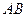 被以原点为圆心的圆
被以原点为圆心的圆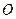 所截得的弦长为
所截得的弦长为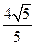 .
.
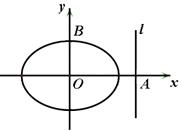
⑴求椭圆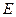 的方程及圆
的方程及圆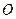 的方程;
的方程;
⑵若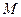 是准线
是准线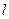 上纵坐标为
上纵坐标为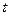 的点,求证:存在一个异于
的点,求证:存在一个异于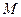 的点
的点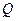 ,对于圆
,对于圆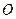 上任意一点
上任意一点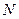 ,有
,有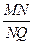 为定值;且当
为定值;且当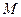 在直线
在直线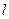 上运动时,点
上运动时,点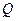 在一个定圆上.
在一个定圆上.
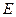 :
: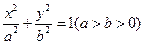 的离心率为
的离心率为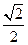 ,且过点
,且过点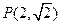 ,设椭圆的右准线
,设椭圆的右准线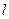 与
与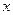 轴的交点为
轴的交点为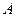 ,椭圆的上顶点为
,椭圆的上顶点为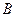 ,直线
,直线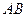 被以原点为圆心的圆
被以原点为圆心的圆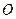 所截得的弦长为
所截得的弦长为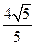 .
.
⑴求椭圆
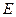 的方程及圆
的方程及圆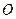 的方程;
的方程;⑵若
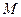 是准线
是准线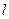 上纵坐标为
上纵坐标为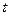 的点,求证:存在一个异于
的点,求证:存在一个异于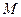 的点
的点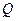 ,对于圆
,对于圆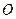 上任意一点
上任意一点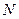 ,有
,有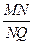 为定值;且当
为定值;且当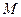 在直线
在直线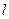 上运动时,点
上运动时,点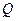 在一个定圆上.
在一个定圆上.⑴椭圆方程: 圆的方程:
圆的方程:
⑵定值为: ,
,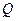 在圆心
在圆心 ,半径为
,半径为 的定圆上
的定圆上
 圆的方程:
圆的方程:
⑵定值为:
 ,
,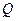 在圆心
在圆心 ,半径为
,半径为 的定圆上
的定圆上略

练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目
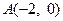 ,
,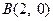 为椭圆
为椭圆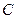 的左、右顶点,
的左、右顶点,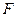 为其右焦点,
为其右焦点,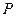 是椭圆
是椭圆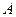 ,
,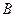 的动点,且
的动点,且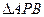 面积的最大值为
面积的最大值为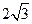 .
. 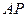 与椭圆在点
与椭圆在点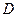 ,当直线
,当直线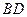

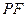 的位置关系,并加以证明.
的位置关系,并加以证明.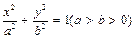 的左、右焦点分别为
的左、右焦点分别为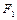 、
、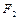 ,离心率
,离心率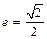 ,右准线方程为
,右准线方程为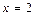 .
.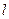 与该椭圆交于M、N两点,且
与该椭圆交于M、N两点,且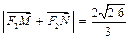 ,求直线
,求直线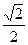 .
. 与椭圆交于A、B两点,O为原点,当△AOB的面积最大时,求直线
与椭圆交于A、B两点,O为原点,当△AOB的面积最大时,求直线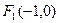 ,
,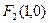 ,离心率为
,离心率为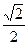 ,Q是椭圆外动点,且
,Q是椭圆外动点,且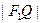 等于椭圆长轴的长,点P是线段
等于椭圆长轴的长,点P是线段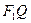 与椭圆的交点,点T是线段
与椭圆的交点,点T是线段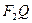 上异于
上异于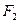 的一点,且
的一点,且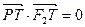 。
。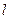 经过
经过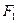 与椭圆交于M,N两点,
与椭圆交于M,N两点,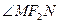 为钝角,求k的取值范围。
为钝角,求k的取值范围。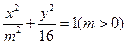 和双曲线
和双曲线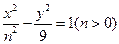 有相同的焦点F1、F2,点P为椭圆和双曲线的一个交点,则|PF1|·|PF2|的值是 。
有相同的焦点F1、F2,点P为椭圆和双曲线的一个交点,则|PF1|·|PF2|的值是 。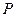 是椭圆
是椭圆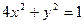 上一点,
上一点,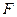 为其中一个焦点,则
为其中一个焦点,则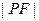 的最
的最 小值为_________.
小值为_________.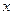 轴上的椭圆
轴上的椭圆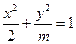 的离心率为
的离心率为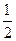 ,则
,则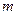 = .
= .