题目内容
16．（Ⅰ）已知${（2x-1）^{10}}={a_0}+{a_1}（x-1）+{a_2}（x-1{）^2}+…+{a_{10}}{（x-1）^{10}}$，其中ai∈R，i=1，2，…10．（i）求a0+a1+a2+…+a10；
（ii）求a7．
（Ⅱ）2017年5月，北京召开“一带一路”国际合作高峰论坛．组委会将甲、乙、丙、丁、戊五名志愿者分配到翻译、导游、礼仪、司机四个不同的岗位，每个岗位至少有一人参加，且五人均能胜任这四个岗位．
（i）若每人不准兼职，则不同的分配方案有几种？
（ii）若甲乙被抽调去别的地方，剩下三人要求每人必兼两职，则不同的分配方案有几种？
分析 （Ⅰ）（i）在（2x-1）10中，令x=2可得 a0+a1+a2+…+a10的值；
（ii）令x-1=y，得出（1+2y）10=a0+a1y+a2y2+…+a10y10，利用二项展开式的通项公式求出a7的值；
（Ⅱ）（i）先从5人中选出2人参加一个岗位，再分4组全排列；
（ii）根据题意，求出4个岗位，3人中每人身兼两职的不同分配方案．
解答 解：（Ⅰ）（i）在（2x-1）10=a0+a1（x-1）+a2（x-1）2+…+a10（x-1）10中，
令x=2可得 a0+a1+a2+…+a10=310，
（ii）令x-1=y，则x=y+1；
∴（1+2y）10=a0+a1y+a2y2+…+a10y10，
∴a7=C10727=15360；
（Ⅱ）（i）每个岗位至少有一人参加，每人不准兼职，则有一个岗位2人参加，
故有分配方案$C_5^2•A_4^4=240$（种）；
（ii）根据题意，4个岗位3个人参加，且每人身兼2职，不同的分配方案有
${{（C}_{4}^{2}）}^{3}$-（${C}_{4}^{2}$+${C}_{4}^{3}$•（${{（C}_{3}^{2}）}^{3}$-${C}_{3}^{2}$））=114（种）．
点评 本题考查了排列、组合，二项式定理的应用问题，是综合题．
练习册系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
16．在如图的程序框图中，若输入的x值为2，则输出的y值为（ ）
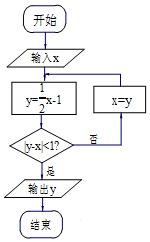
| A． | 0 | B． | $\frac{1}{2}$ | C． | -$\frac{3}{2}$ | D． | -1 |
11．△ABC的内角A、B、C的对边分别为a、b、c．已知a=$\sqrt{5}$，b=3，cosA=$\frac{2}{3}$，则c=（ ）
| A． | 3 | B． | $\sqrt{3}$ | C． | 2 | D． | $\sqrt{2}$ |
1．若用半径为2的半圆卷成一个圆锥，则圆锥的体积为（ ）
| A． | $\sqrt{3}π$ | B． | $\frac{{\sqrt{3}π}}{3}$ | C． | $\frac{{\sqrt{5}π}}{3}$ | D． | $\sqrt{5}π$ |
5．若?x∈R，函数f（x）=2mx2-2（4-m）x+1与g（x）=mx的值至少有一个为正数，则实数m的取值范围为（ ）
| A． | （0，4] | B． | （0，8） | C． | （2，5） | D． | （-∞，0） |