题目内容
15.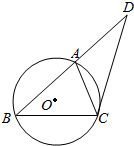 如图,圆O是△ABC的外接圆,AB=BC,DC是圆O的切线,若AD=4,CD=6,则AC的长为( )
如图,圆O是△ABC的外接圆,AB=BC,DC是圆O的切线,若AD=4,CD=6,则AC的长为( )| A. | 5 | B. | 4 | C. | $\frac{10}{3}$ | D. | 3 |
分析 由切割线定理求出AB=BC=5,由弦切角定理得到△BCD∽△CAD,由此能求出AC.
解答  解:∵圆O是△ABC的外接圆,AB=BC,DC是圆O的切线,AD=4,CD=6,
解:∵圆O是△ABC的外接圆,AB=BC,DC是圆O的切线,AD=4,CD=6,
∴∠ACD=∠ABC,CD2=AD•BD,即36=4(4+AB),
解得AB=5,∴BC=5
∵∠ACD=∠ABC,∠D=∠D,
∴△BCD∽△CAD,
∴$\frac{AC}{BC}=\frac{DC}{BD}=\frac{AD}{DC}$,
∴$\frac{AC}{5}=\frac{6}{9}$,解得AC=$\frac{10}{3}$.
故选:C.
点评 本题考查与圆有关的线段长的求法,是基础题,解题时要认真审题,注意切割线定理和弦切角定理的合理运用.

练习册系列答案
相关题目
 已知点D、E、F分别为△ABC的边BC、CA、AB上的点,AD、BE、CF相交于点P,且AE=EC,BF=2FA.
已知点D、E、F分别为△ABC的边BC、CA、AB上的点,AD、BE、CF相交于点P,且AE=EC,BF=2FA.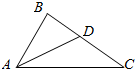 如图,在△ABC中,∠B=$\frac{π}{2}$,∠BAC的平分线交BC于点D,AD=$\sqrt{2}$,AC=$\sqrt{6}$,则△ABC的面积为$\frac{3\sqrt{3}}{4}$.
如图,在△ABC中,∠B=$\frac{π}{2}$,∠BAC的平分线交BC于点D,AD=$\sqrt{2}$,AC=$\sqrt{6}$,则△ABC的面积为$\frac{3\sqrt{3}}{4}$.