题目内容
7.已知椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$(a>b>0)的半焦距为c(c>0),左焦点为F,右顶点为A,抛物线${y^2}=\frac{15}{8}(a+c)x$与椭圆交于M,N两点,若四边形AMFN是菱形,则椭圆的离心率是( )| A. | $\frac{8}{15}$ | B. | $\frac{4}{15}$ | C. | $\frac{2}{3}$ | D. | $\frac{1}{2}$ |
分析 根据菱形的性质,求得M的横坐标,代入抛物线方程和椭圆方程,根据椭圆的性质.即可求得椭圆的离心率.
解答 解:由题意知,椭圆的左焦点为F(-c,0),右顶点为A(a,0),由四边形AMFN是菱形,
∴M、N两点的横坐标为x=$\frac{a-c}{2}$,将x代入抛物线中得:y2=$\frac{15}{16}$(a2-c2),
将M、N两点的横坐标代入椭圆方程中可得:$\frac{(a-c)^{2}}{4{a}^{2}}+\frac{15}{16}\frac{({a}^{2}-{c}^{2})}{{b}^{2}}=1$,
由b2=a2-c2,则$\frac{(a-c)^{2}}{4{a}^{2}}$=$\frac{1}{16}$,得$\frac{a-c}{a}$=$\frac{1}{2}$,即1-e=$\frac{1}{2}$,则e=$\frac{1}{2}$,
∴椭圆的离心率为e=$\frac{1}{2}$,
故选:D.
点评 本题考查椭圆及抛物线的方程,椭圆的简单几何性质,考查计算能力,属于中档题.

练习册系列答案
相关题目
15.已知函数f(x)=sinωx-$\sqrt{3}$cosωx(ω>0),若方程f(x)=-1在(0,π)上有且只有四个实数根,则实数ω的取值范围为( )
| A. | ($\frac{13}{6}$,$\frac{7}{2}$] | B. | ($\frac{7}{2}$,$\frac{25}{6}$] | C. | ($\frac{25}{6}$,$\frac{11}{2}$] | D. | ($\frac{11}{2}$,$\frac{37}{6}$] |
2.心理学家分析发现视觉和空间能力与性别有关,某数学兴趣小组为了验证这个结论,从兴趣小组中用分层抽样的方法抽取50名同学(男30,女20),给所选的同学几何题和代数题各一题,让各位同学自由选择一题进行解答,选题情况如表(单位:人)
(1)能否据此判断有97%的把握认为视觉和空间能力与性别有关
(2)经过多次测试后,甲每次解答一道几何题所用的时间在5-7分钟,乙每次解答一道几何题所用的时间在6-8分钟,现甲乙解同一道几何题,求乙比甲先解答完成的概率
(3)现从选择做几何题的8名女生中任意抽取两人对她们的大题情况进行全程研究,记甲、乙两女生被抽到的人数为X,求X的分布列及数学期E(X)
附表及公式
k2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$.
| 几何体 | 代数题 | 总计 | |
| 男同学 | 22 | 8 | 30 |
| 女同学 | 8 | 12 | 20 |
| 总计 | 30 | 20 | 50 |
(2)经过多次测试后,甲每次解答一道几何题所用的时间在5-7分钟,乙每次解答一道几何题所用的时间在6-8分钟,现甲乙解同一道几何题,求乙比甲先解答完成的概率
(3)现从选择做几何题的8名女生中任意抽取两人对她们的大题情况进行全程研究,记甲、乙两女生被抽到的人数为X,求X的分布列及数学期E(X)
附表及公式
| P(k2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.10 | 0.005 | 0.001 |
| k0 | 2.072 | 2.706 | 3.481 | 5.024 | 6.635 | 7.879 | 10.828 |
19.已知$\overrightarrow{a}$=(1,cosα),$\overrightarrow{b}$=(sinα,1),0<α<π,若$\vec a⊥\vec b$,则α=( )
| A. | $\frac{2π}{3}$ | B. | $\frac{3π}{4}$ | C. | $\frac{π}{4}$ | D. | $\frac{π}{6}$ |
16.已知全集U=R,A={x|x2-2x<0},B={x|2x≥2},则A∩(∁UB)=( )
| A. | {x|0<x<2} | B. | {x|0<x<1} | C. | {x|0<x≤1} | D. | {x|0<x≤2} |
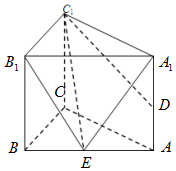 如图,已知直三棱柱ABC-A1B1C1的侧棱长为2,底面△ABC是等腰直角三角形,且∠ACB=90°,AC=2,D是AA1的中点.
如图,已知直三棱柱ABC-A1B1C1的侧棱长为2,底面△ABC是等腰直角三角形,且∠ACB=90°,AC=2,D是AA1的中点.