题目内容
18.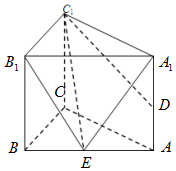 如图,已知直三棱柱ABC-A1B1C1的侧棱长为2,底面△ABC是等腰直角三角形,且∠ACB=90°,AC=2,D是AA1的中点.
如图,已知直三棱柱ABC-A1B1C1的侧棱长为2,底面△ABC是等腰直角三角形,且∠ACB=90°,AC=2,D是AA1的中点.(Ⅰ)求异面直线AB和C1D所成角的余弦值;
(Ⅱ)若E为AB上一点,试确定点E在AB上的位置,使得A1E⊥C1D;
(Ⅲ)在(Ⅱ)的条件下,求点D到平面B1C1E的距离.
分析 (I)取CC1的中点F,连接AF,BF,在△ABF中,利用余弦定理计算cos∠BAF即可得出结论;
(II)过E作NE⊥AC于N,连接A1N,则由线面垂直的性质可得A1N⊥C1D,通过计算N的位置即可得出E的位置;
(III)连接C1N,则可证面B1C1NE⊥平面AA1C1C,过点D作DH⊥C1N,则根据面面垂直的性质得出DH即为D到平面B1C1E的距离,在△C1DN中计算DH即可得出.
解答 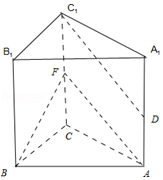 解:(Ⅰ)取CC1的中点F,连接AF,BF,则AF∥C1D.
解:(Ⅰ)取CC1的中点F,连接AF,BF,则AF∥C1D.
∴∠BAF为异面直线AB与C1D所成的角或其补角.
∵△ABC为等腰直角三角形,AC=2,∴AB=2$\sqrt{2}$.
又∵CC1=2,∴AF=BF=$\sqrt{5}$.
∵cos∠BAF=$\frac{A{F}^{2}+A{B}^{2}-B{F}^{2}}{2AF•AB}$=$\frac{\sqrt{10}}{5}$,
即异面直线AB与C1D所成的角的余弦值为$\frac{\sqrt{10}}{5}$.
(Ⅱ)过E作NE⊥AC于N,连接A1N,
∵AA1⊥平面ABC,EN?平面ABC,
∴AA1⊥EN,又AC⊥EN,AC∩AA1=A,
∴EN⊥平面AA1C1C,又C1D?平面AA1C1C,
∴EN⊥C1D,
又A1E⊥C1D,EN∩A1E=E,
∴C1D⊥平面A1EN,∵A1N?平面A1EN,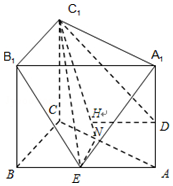
∴A1N⊥C1D.
∵四边形AA1C1C为正方形,
∴N为AC的中点,又BC⊥AC,EN⊥AC,
∴E点为AB的中点.
(Ⅲ)连接C1N,
由(II)可知EN⊥平面AA1C1C,又EN?平面ENC1B1,
∴面B1C1NE⊥平面AA1C1C.
过点D作DH⊥C1N,垂足为H,则DH⊥平面B1C1NE,
∴DH为点D到平面B1C1E的距离.
在正方形AA1C1C中,∵D,N分别是AA1,AC的中点,
∴DN=$\sqrt{2}$,C1D=C1N=$\sqrt{5}$,
∴cos∠DC1N=$\frac{{C}_{1}{D}^{2}+{C}_{1}{N}^{2}-D{N}^{2}}{2{C}_{1}D•{C}_{1}N}$=$\frac{4}{5}$,∴sin∠DC1N=$\frac{3}{5}$.
∴DH=C1Dsin∠DC1N=$\frac{3\sqrt{5}}{5}$,
即点D到平面B1C1E的距离$\frac{3\sqrt{5}}{5}$.
点评 本题考查了线面垂直的判定与性质,空间角与空间距离的计算,属于中档题.

| A. | $\frac{8}{7}$ | B. | $-\frac{8}{7}$ | C. | $\frac{10}{7}$ | D. | $-\frac{10}{7}$ |
| A. | $\frac{8}{15}$ | B. | $\frac{4}{15}$ | C. | $\frac{2}{3}$ | D. | $\frac{1}{2}$ |
 如图,矩形ABCD中,AB=2AD=2,E为边AB的中点,将△ADE沿直线DE翻转成△A1DE,若M为线段A1C的中点,则在△ADE翻转过程中,对于下列说法:
如图,矩形ABCD中,AB=2AD=2,E为边AB的中点,将△ADE沿直线DE翻转成△A1DE,若M为线段A1C的中点,则在△ADE翻转过程中,对于下列说法: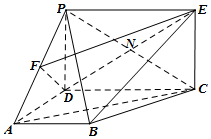 如图,PD垂直于梯形ABCD所在的平面,∠ADC=∠BAD=90°.F为PA中点,PD=$\sqrt{2}$,AB=AD=$\frac{1}{2}$CD=1. 四边形PDCE为矩形,线段PC交DE于点N.
如图,PD垂直于梯形ABCD所在的平面,∠ADC=∠BAD=90°.F为PA中点,PD=$\sqrt{2}$,AB=AD=$\frac{1}{2}$CD=1. 四边形PDCE为矩形,线段PC交DE于点N.