题目内容
如图,已知长方体ABCD-A1B1C1D1中,AB=3,BC=2,CC1=5,E是棱CC1上不同于端点的点,且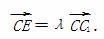
(1) 当∠BEA1为钝角时,求实数λ的取值范围;
(2) 若λ= ,记二面角B1-A1B-E的的大小为θ,求|cosθ|.
,记二面角B1-A1B-E的的大小为θ,求|cosθ|.
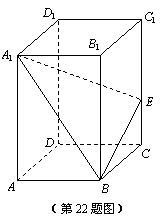 |
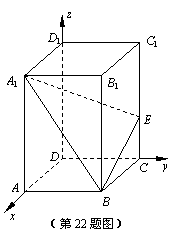
解:(1)以D为原点,DA为x轴,DC为y轴,DD1为z轴,建立如图所示的空间直角坐标系.
由题设,知B(2,3,0),A1(2,0,5),C(0,3,0),C1(0,3,5).
 因为
因为 ,所以E(0,3,5λ).
,所以E(0,3,5λ).
从而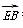 =(2,0,-5λ),
=(2,0,-5λ),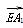 =(2,-3,5-5λ)
=(2,-3,5-5λ)
当∠BEA1为钝角时,cos∠BEA1<0,
所以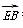 ·
·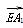 <0,即2×2-5λ(5-5λ)<0,
<0,即2×2-5λ(5-5λ)<0,
解得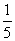 <λ<
<λ<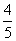 .
.
即实数λ的取值范围是(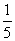 ,
,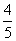 ).
).
(2)当λ= 时,
时,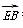 =(2,0,-2),
=(2,0,-2), =(2,-3,3).
=(2,-3,3).
设平面BEA1的一个法向量为n1=(x,y,z),
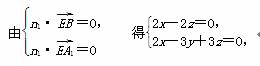 取x=1,得y=
取x=1,得y=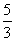 ,z=1,
,z=1,
所以平面BEA1的一个法向量为n1=(1,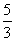 ,1).
,1).
易知,平面BA1B1的一个法向量为n2=(1,0,0).
因为cos< n1,n2>=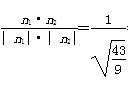 =
=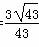 ,
,
从而|cosθ|=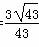 .
.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
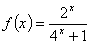
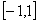 上的解析式;(4分)
上的解析式;(4分) 函数
函数 在区间
在区间 上是单调递增函数;命题
上是单调递增函数;命题 不等式
不等式 对任意实数
对任意实数 恒成立.若
恒成立.若 是真命题,且
是真命题,且 为假命题,求实数
为假命题,求实数 的取值范围.
的取值范围.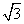 ,则|
,则| +
+ |的最大值是 .
|的最大值是 . R.
R. β,则l∥m.
β,则l∥m.
 的右顶点A作斜率为
的右顶点A作斜率为 的直线,该直线与双曲线的两条渐近线的交点分别为B, C.若
的直线,该直线与双曲线的两条渐近线的交点分别为B, C.若 ,则双曲线的离心率是
,则双曲线的离心率是  B.
B. C.
C. D.
D.
 ,则
,则 的值为 .
的值为 .