题目内容
已知平行四边形的顶点坐标依次为A（-1，0），B（0，
），C（1，0），D（0，-
），若动点M与点B、点D连线的斜率之积为-
，则 MA+MC= ．
| 3 |
| 3 |
| 3 |
| 4 |
考点：直线的斜率
专题：直线与圆
分析：由题意可得
•
=-
，整理可得动点M在A、C为焦点的椭圆上，由椭圆的定义可得．
y-
| ||
| x |
y+
| ||
| x |
| 3 |
| 4 |
解答：
解：设M（x，y），则
•
=-
，
整理可得
+
=1，
∴动点M在A、C为焦点的椭圆上，
∴MA+MC=2a=4
故答案为：4．
y-
| ||
| x |
y+
| ||
| x |
| 3 |
| 4 |
整理可得
| x2 |
| 4 |
| y2 |
| 3 |
∴动点M在A、C为焦点的椭圆上，
∴MA+MC=2a=4
故答案为：4．
点评：本题考查直线的向量，涉及椭圆的定义和简单应用，属基础题．
练习册系列答案
相关题目
如图，在四棱柱ABCD-A1B1C1D1中，A1A⊥底面ABCD，∠BAD=90°，AD∥BC，且A1A=AD=2BC=2，AB=1．点E在棱AB上，平面A1EC与棱C1D1相交于点F．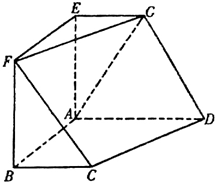
如图，在六面体ABCDEFG中，平面EFG∥平面ABCD，AE⊥平面ABCD，EF⊥AE，AE=AB=AD，EG=BC，且EF=2EG．
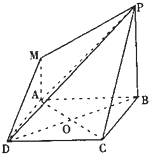如图，四边形ABCD是正方形，MA⊥平面ABCD，MA∥PB，PB=AB=2MA=2．