题目内容
已知△ABC的内角为A、B、C,其对边分别为a、b、c,B为锐角,向量m=(2sin B,-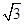 ),n=
),n=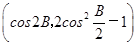 ,且m∥n
,且m∥n
(1)求角B的大小;
(2)如果b=2,求S△ABC的最大值.
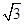 ),n=
),n=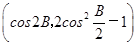 ,且m∥n
,且m∥n(1)求角B的大小;
(2)如果b=2,求S△ABC的最大值.
(1) (2)
(2)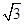
 (2)
(2)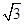
(1)m∥n⇒2sin B· +
+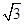 cos 2B=0
cos 2B=0
⇒sin 2B+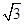 cos 2B=0⇒2sin
cos 2B=0⇒2sin =0(B为锐角)⇒2B=
=0(B为锐角)⇒2B= ⇒B=
⇒B= .
.
(2)cos B= ⇒ac=a2+c2-4≥2ac-4⇒ac≤4.
⇒ac=a2+c2-4≥2ac-4⇒ac≤4.
S△ABC= a·c·sin B≤
a·c·sin B≤ ×4×
×4× =
=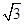 .
.
 +
+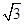 cos 2B=0
cos 2B=0⇒sin 2B+
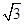 cos 2B=0⇒2sin
cos 2B=0⇒2sin =0(B为锐角)⇒2B=
=0(B为锐角)⇒2B= ⇒B=
⇒B= .
.(2)cos B=
 ⇒ac=a2+c2-4≥2ac-4⇒ac≤4.
⇒ac=a2+c2-4≥2ac-4⇒ac≤4.S△ABC=
 a·c·sin B≤
a·c·sin B≤ ×4×
×4× =
=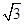 .
.
练习册系列答案
相关题目
 到
到 ,方位角(从正北方向顺时针转到
,方位角(从正北方向顺时针转到 方向所成的角)是
方向所成的角)是 ,距离是3km;从
,距离是3km;从 ,方位角是110°,距离是3km;从
,方位角是110°,距离是3km;从 ,方位角是140°,距离是(
,方位角是140°,距离是( )km.试画出大致示意图,并计算出从A到D的方位角和距离(结果保留根号).
)km.试画出大致示意图,并计算出从A到D的方位角和距离(结果保留根号). 中,
中, 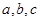 分别是角
分别是角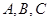 的对边,且
的对边,且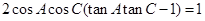 .
.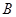 的大小; (2)若
的大小; (2)若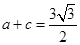 ,
,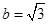 ,求
,求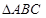 中,三个内角
中,三个内角 所对边的长分别为
所对边的长分别为 ,已知
,已知 .
. ,若
,若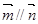 ,求
,求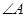 .
.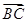 ·
·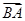 +c
+c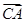 ·
·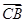 =0.
=0.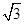 ,试求
,试求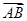 ·
·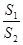 的最小值.
的最小值.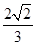 ,AB=3
,AB=3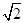 ,AD=3,则BD的长为________.
,AD=3,则BD的长为________.