题目内容
求(n+1)(n+2)…(n+n)=2n′1′2′3′…(2n─1)(n∈N),从“k到k+1”左端应增乘的代数式为分析:首先分析题目求从“k到k+1”左端应增乘的代数式,可把n=k,n=k+1分别代入等式左边(n+1)(n+2)…(n+n),相比较求出增乘的代数式即可得到答案.
解答:解:当n=k时 等式左边=(k+1)(k+2)…(k+k).
当n=k+1时 等式左边=[(k+1)+1][(k+1)+2]…[(k+1)+k][(k+1)+k+1].
比原来多了两项[(k+1)+k][(k+1)+k+1]=2(2k+1)(k+1),但是少了一项 k+1
所以两式相除得
=2(2k+1),
即答案为2(2k+1).
当n=k+1时 等式左边=[(k+1)+1][(k+1)+2]…[(k+1)+k][(k+1)+k+1].
比原来多了两项[(k+1)+k][(k+1)+k+1]=2(2k+1)(k+1),但是少了一项 k+1
所以两式相除得
| 2(2k+1)(k+1) |
| k+1 |
即答案为2(2k+1).
点评:此题主要考查学生计算的灵活性,题目覆盖的知识点少,计算量小,属于基础性试题.

练习册系列答案
 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案
相关题目
 (2012•闵行区一模)将边长分别为1、2、3、…、n、n+1、…(n∈N*)的正方形叠放在一起,形成如图所示的图形,由小到大,依次记各阴影部分所在的图形为第1个、第2个、…、第n个阴影部分图形.设前n个阴影部分图形的面积的平均值为f(n).记数列{an}满足a1=1,
(2012•闵行区一模)将边长分别为1、2、3、…、n、n+1、…(n∈N*)的正方形叠放在一起,形成如图所示的图形,由小到大,依次记各阴影部分所在的图形为第1个、第2个、…、第n个阴影部分图形.设前n个阴影部分图形的面积的平均值为f(n).记数列{an}满足a1=1,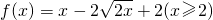
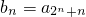 ,求数列{bn}前n项和Tn.
,求数列{bn}前n项和Tn.