题目内容
已知函数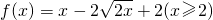
(1)求反函数f-1(x);
(2)若数列{an}(an>0)的前n项和Sn满足:a1=2,Sn=f-1(Sn-1)(n≥2)
①求数列{an}的通项公式.
②令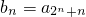 ,求数列{bn}前n项和Tn.
,求数列{bn}前n项和Tn.
解:(1)∵函数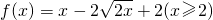
∴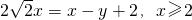 ,
,
两边平方,得8x=x2+y2+4-2xy-4y+4x,
整理,得x2-(2y+4)x+y2-4y+4=0,x≥2.
∴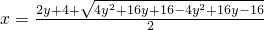
=y+2+2 =
= ,
,
x,y互换,得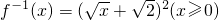 .
.
(2)①∵a1=2,Sn=f-1(Sn-1)(n≥2)
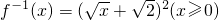 .
.
∴
∴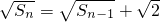 ,
,
∵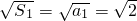 ,
,
∴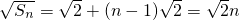 ,
,
∴Sn=2n2,
∵a1=S1=2,
an=Sn-Sn-1=2n2-2(n-1)2=4n-2,
当n=1时,4n-2=2=a1,
∴an=4n-2.
②∵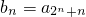 ,
,
且an=4n-2.
∴bn=4(2n+n)-2,
∴Tn=4(1+2+3+…+n)+4(2+22+23+…+2n)-2n
∴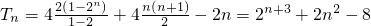 .
.
分析:(1)函数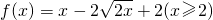 ,得
,得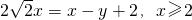 ,两边平方,并整理,得x2-(2y+4)x+y2-4y+4=0,x≥2.所以x=y+2+2
,两边平方,并整理,得x2-(2y+4)x+y2-4y+4=0,x≥2.所以x=y+2+2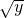 =
=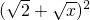 ,x,y互换,得反函数f-1(x).
,x,y互换,得反函数f-1(x).
(2)①由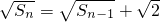 ,知Sn=2n2,由此能求出数列{an}的通项公式.
,知Sn=2n2,由此能求出数列{an}的通项公式.
②由bn=4(2n+n)-2,由求出数列{bn}前n项和Tn.
点评:本题考查反函数的求法、数列通项公式的求法和数列的前n项和的求法,解题时要认真审题,仔细解答,注意合理地进行等价转化.
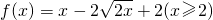
∴
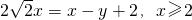 ,
,两边平方,得8x=x2+y2+4-2xy-4y+4x,
整理,得x2-(2y+4)x+y2-4y+4=0,x≥2.
∴
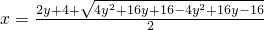
=y+2+2
 =
= ,
,x,y互换,得
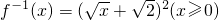 .
.(2)①∵a1=2,Sn=f-1(Sn-1)(n≥2)
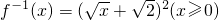 .
.∴

∴
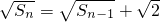 ,
,∵
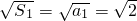 ,
,∴
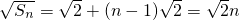 ,
,∴Sn=2n2,
∵a1=S1=2,
an=Sn-Sn-1=2n2-2(n-1)2=4n-2,
当n=1时,4n-2=2=a1,
∴an=4n-2.
②∵
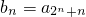 ,
,且an=4n-2.
∴bn=4(2n+n)-2,
∴Tn=4(1+2+3+…+n)+4(2+22+23+…+2n)-2n
∴
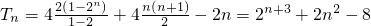 .
.分析:(1)函数
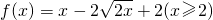 ,得
,得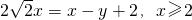 ,两边平方,并整理,得x2-(2y+4)x+y2-4y+4=0,x≥2.所以x=y+2+2
,两边平方,并整理,得x2-(2y+4)x+y2-4y+4=0,x≥2.所以x=y+2+2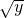 =
=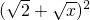 ,x,y互换,得反函数f-1(x).
,x,y互换,得反函数f-1(x).(2)①由
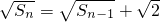 ,知Sn=2n2,由此能求出数列{an}的通项公式.
,知Sn=2n2,由此能求出数列{an}的通项公式.②由bn=4(2n+n)-2,由求出数列{bn}前n项和Tn.
点评:本题考查反函数的求法、数列通项公式的求法和数列的前n项和的求法,解题时要认真审题,仔细解答,注意合理地进行等价转化.

练习册系列答案
 综合自测系列答案
综合自测系列答案
相关题目
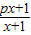 ,若由函数f(x)确定的数列{an}的自反数列为{bn},求an;
,若由函数f(x)确定的数列{an}的自反数列为{bn},求an; (cn+
(cn+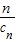 ).写出Sn表达式,并证明你的结论;
).写出Sn表达式,并证明你的结论;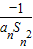 ,Dn是数列{dn}的前n项和,且Dn>loga(1-2a)恒成立,求a的取值范围.
,Dn是数列{dn}的前n项和,且Dn>loga(1-2a)恒成立,求a的取值范围.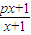 ,若由函数f(x)确定的数列{an}的自反数列为{bn},求an;
,若由函数f(x)确定的数列{an}的自反数列为{bn},求an; (cn+
(cn+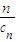 ).写出Sn表达式,并证明你的结论;
).写出Sn表达式,并证明你的结论;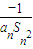 ,Dn是数列{dn}的前n项和,且Dn>loga(1-2a)恒成立,求a的取值范围.
,Dn是数列{dn}的前n项和,且Dn>loga(1-2a)恒成立,求a的取值范围.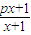 ,若由函数f(x)确定的数列{an}的自反数列为{bn},求an;
,若由函数f(x)确定的数列{an}的自反数列为{bn},求an; (cn+
(cn+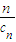 ).写出Sn表达式,并证明你的结论;
).写出Sn表达式,并证明你的结论;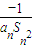 ,Dn是数列{dn}的前n项和,且Dn>loga(1-2a)恒成立,求a的取值范围.
,Dn是数列{dn}的前n项和,且Dn>loga(1-2a)恒成立,求a的取值范围.