Question

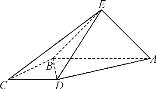
【题目】如图，在三棱锥P-ABC中，，平面平面ABC，点D在线段BC上，且，F是线段AB的中点，点E是PD上的动点.

（1）证明：.

（2）当EF//平面PAC时，求三棱锥C-DEF的体积.

Answer 1

【答案】(1)证明见解析 ；(2) .

【解析】

（1）利用面面垂直的性质定理证得平面，由此证得.通过中位线和等腰三角形的性质，证得，由此证得平面，进而证得l;（2）利用面面平行的判定定理证得，由此求得点到平面的距离等于点到平面距离的三分之一，进而利用，求得三棱锥的体积.

（1）连接，因为，F为AB的中点，

所以.

又平面平面ABC，平面平面，

所以平面ABC，从而

设BC的中点H，连接,因为，DF是的中位线，

所以.

因为，是中点，，所以

所以平面PDF

因为平面PDF，所以

（2）设点E到平面ABC的距离为，由（1）知，则平面，而平面，，所以平面平面，

所以.

所以，

又，

所以