Question

【题目】已知圆C1：x2+y2=r2（r＞0）与直线l0：y= 相切，点A为圆C1上一动点，AN⊥x轴于点N，且动点M满足 ，设动点M的轨迹为曲线C．
（1）求动点M的轨迹曲线C的方程；
（2）若直线l与曲线C相交于不同的两点P、Q且满足以PQ为直径的圆过坐标原点O，求线段PQ长度的取值范围．

Answer 1

【答案】
（1）解：设动点M（x，y），A（x0，y0），由于AN⊥x轴于点N．∴N（x0，0）．

又圆 与直线 即 相切，∴ ．

∴圆 ．

由题意， ，得 ，

∴ ．

∴ ，

即∴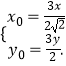

将 代入x2+y2=9，得曲线C的方程为 ．

（2）⑴假设直线l的斜率存在，设其方程为y=kx+m，设P（x1，y1），Q（x2，y2），

联立 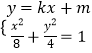，可得（1+2k2）x2+4kmx+2m2﹣8=0．

由求根公式得 ．（*）

∵以PQ为直径的圆过坐标原点O，∴ ．即 ．

∴x1x2+y1y2=0．即∴x1x2+（kx1+m）（kx2+m）=0．

化简可得， ．

将（*）代入可得 ，即3m2﹣8k2﹣8=0．

即 ，又 ．

将 代入，可得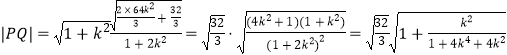

= ．

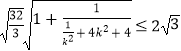∴当且仅当 ，即 时等号成立．又由 ，∴ ，

∴ ．

⑵若直线l的斜率不存在，因以PQ为直径的圆过坐标原点O，故可设OP所在直线方程为y=x，

联立 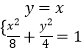解得 ，同理求得 ，

故 ．综上，得 ．

【解析】1、由求轨迹方程的方法可设动点M（x，y），A（x0，y0），由于AN⊥x轴于点N．∴N（x0，0）根据题意可得
圆 ． += ( 2 2 2 ) ，得 ( x ， y ) + 2 ( x x 0， y y 0 ) = ( 2 2 2 ) ( x 0 ， 0 ) ，

∴ ．联立方程可得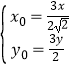,将点A代入双曲线的方程的
2、假设存在这样的直线设其方程为y=kx+m，设P（x1，y1），Q（x2，y2），联立 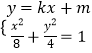，可得（1+2k2）x2+4kmx+2m2﹣8=0．
由求根公式得,由题意可得,,∴x1x2+y1y2=0．即∴x1x2+（kx1+m）（kx2+m）=0．即 由题意可得，当且仅当时等号成立即。若直线l的斜率不存在，因以PQ为直径的圆过坐标原点O，故可设OP所在直线方程为y=x，联立方程可得同理求得故得结果。