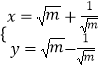Question

【题目】如图，设椭圆C： =1（a＞b＞0）的离心率为 ，A，B分别为椭圆C的左、右顶点，F为右焦点．直线y=6x与C的交点到y轴的距离为 ，过点B作x轴的垂线l，D为l 上异于点B的一点，以BD为直径作圆E．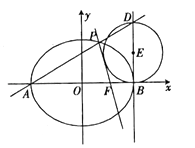

（1）求C 的方程；
（2）若直线AD与C的另一个交点为P，证明PF与圆E相切．

Answer 1

【答案】
（1）解：由题意可知， ，∴a=2c，

又a2=b2+c2，则b2=3c2．

设椭圆C的方程为 ，

联立 ，解得x= ，∴c=1，a=2，b2=3．

故椭圆C的方程为 ；

（2）证明：由（1）可得F（1，0），设圆E的圆心为（2，t）（t≠0），则D（2，2t），

则圆E的半径R=t．

直线AD的方程为y= ．

联立 ，得（3+t2）x2+4t2x+4t2﹣12=0．

由 ，得 ， ．

直线PF的方程为 ，

即2tx+（t2﹣1）y﹣2t=0．

∵点E（2，t）到直线PF的距离为d= ，

∴直线PF与圆E相切．

【解析】（1）根据题意得到,再联立直线方程，得到交点坐标，结合距离为，可得到椭圆的方程，（2）由椭圆方程得出焦点F的坐标，设其圆E的圆心坐标和半径，得到直线AD的方程，联立椭圆方程得到P点的坐标，表示出PF的直线方程，根据点E到PF的距离不难得到PF与圆E相切.