题目内容
在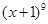 的二项展开式中任取
的二项展开式中任取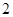 项,
项,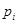 表示取出的
表示取出的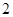 项中有
项中有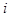 项系数为奇数的概率. 若用随机变量
项系数为奇数的概率. 若用随机变量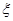 表示取出的
表示取出的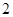 项中系数为奇数的项数
项中系数为奇数的项数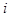 ,则随机变量
,则随机变量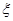 的数学期望
的数学期望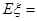 ( )
( )
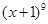 的二项展开式中任取
的二项展开式中任取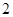 项,
项,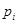 表示取出的
表示取出的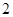 项中有
项中有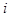 项系数为奇数的概率. 若用随机变量
项系数为奇数的概率. 若用随机变量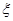 表示取出的
表示取出的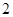 项中系数为奇数的项数
项中系数为奇数的项数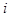 ,则随机变量
,则随机变量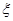 的数学期望
的数学期望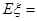 ( )
( )A.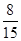 | B.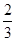 | C.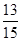 | D.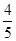 |
D
试题分析:根据题意,由于在
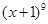 的二项展开式中任取
的二项展开式中任取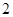 项,
项,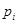 表示取出的
表示取出的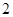 项中有
项中有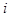 项系数为奇数的概率. 因为各项的系数为
项系数为奇数的概率. 因为各项的系数为 ,用随机变量
,用随机变量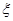 表示取出的
表示取出的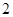 项中系数为奇数的项数
项中系数为奇数的项数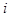 ,则随机变量
,则随机变量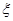 的数学期望
的数学期望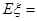
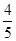 ,故答案为D.
,故答案为D.点评:主要是考查了二项式定理以及随机变量分布列的运用,属于基础题。

练习册系列答案
相关题目
 人组成男子篮球队代表所在区参赛,队员来源人数如下表:
人组成男子篮球队代表所在区参赛,队员来源人数如下表:
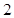
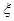 ,求随机变量
,求随机变量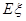 .
.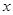 ,现从袋中随机摸出2个球,并计算摸出的这2个球上的数字之和,记录后将小球放回袋中搅匀,进行重复试验。记A事件为“数字之和为7”.试验数据如下表
,现从袋中随机摸出2个球,并计算摸出的这2个球上的数字之和,记录后将小球放回袋中搅匀,进行重复试验。记A事件为“数字之和为7”.试验数据如下表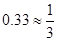 )
)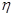 元,求
元,求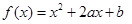
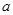 是从
是从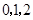 三个数中任取的一个数,
三个数中任取的一个数,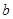 是从
是从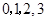 四个数中任取的一个数,求
四个数中任取的一个数,求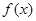 为偶函数的概率;
为偶函数的概率;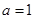 ,
,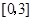 任取的一个数,求方程
任取的一个数,求方程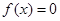 有实根的概率.
有实根的概率.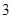 人,每人回答一个问题,答对者为本队赢得一分,答错得零分。假设甲队中每人答对的概率均为
人,每人回答一个问题,答对者为本队赢得一分,答错得零分。假设甲队中每人答对的概率均为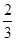 ,乙队中
,乙队中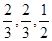 且各人正确与否相互之间没有影响.用
且各人正确与否相互之间没有影响.用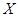 表示甲队的总得分.
表示甲队的总得分.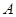 表示“甲、乙两个队总得分之和等于
表示“甲、乙两个队总得分之和等于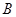 表示“甲队总得分大于乙队总得分”这一事件,求
表示“甲队总得分大于乙队总得分”这一事件,求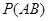 。
。 服从正态分布
服从正态分布 ,且
,且 ,则
,则 等于 .
等于 . 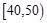 ,
, ,…,
,…, 后得到如下频率分布直方图.
后得到如下频率分布直方图.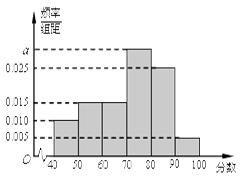
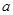 的值
的值