题目内容
甲乙两队参加知识竞赛,每队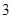 人,每人回答一个问题,答对者为本队赢得一分,答错得零分。假设甲队中每人答对的概率均为
人,每人回答一个问题,答对者为本队赢得一分,答错得零分。假设甲队中每人答对的概率均为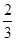 ,乙队中
,乙队中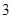 人答对的概率分别为
人答对的概率分别为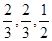 且各人正确与否相互之间没有影响.用
且各人正确与否相互之间没有影响.用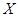 表示甲队的总得分.
表示甲队的总得分.
(Ⅰ)求随机变量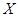 分布列
分布列
(Ⅱ)用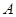 表示“甲、乙两个队总得分之和等于
表示“甲、乙两个队总得分之和等于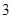 ”这一事件,用
”这一事件,用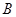 表示“甲队总得分大于乙队总得分”这一事件,求
表示“甲队总得分大于乙队总得分”这一事件,求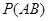 。
。
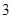 人,每人回答一个问题,答对者为本队赢得一分,答错得零分。假设甲队中每人答对的概率均为
人,每人回答一个问题,答对者为本队赢得一分,答错得零分。假设甲队中每人答对的概率均为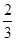 ,乙队中
,乙队中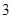 人答对的概率分别为
人答对的概率分别为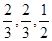 且各人正确与否相互之间没有影响.用
且各人正确与否相互之间没有影响.用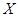 表示甲队的总得分.
表示甲队的总得分.(Ⅰ)求随机变量
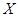 分布列
分布列 (Ⅱ)用
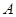 表示“甲、乙两个队总得分之和等于
表示“甲、乙两个队总得分之和等于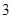 ”这一事件,用
”这一事件,用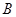 表示“甲队总得分大于乙队总得分”这一事件,求
表示“甲队总得分大于乙队总得分”这一事件,求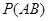 。
。(1)根据题意,由于甲队中每人答对的概率均为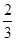 ,且各人正确与否相互之间没有影响,那么用
,且各人正确与否相互之间没有影响,那么用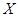 表示甲队的总得分,则可知x的可能取值为0,1,2,3,
表示甲队的总得分,则可知x的可能取值为0,1,2,3,
根据期望公式得到
(2)
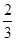 ,且各人正确与否相互之间没有影响,那么用
,且各人正确与否相互之间没有影响,那么用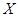 表示甲队的总得分,则可知x的可能取值为0,1,2,3,
表示甲队的总得分,则可知x的可能取值为0,1,2,3, | 0 | 1 | 2 | 3 |
| P |  |  |  |  |

(2)

试题分析:(1)
 | 0 | 1 | 2 | 3 |
| P |  |  |  |  |

(2)根据题意,由于用
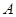 表示“甲、乙两个队总得分之和等于
表示“甲、乙两个队总得分之和等于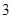 ”这一事件,用
”这一事件,用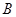 表示“甲队总得分大于乙队总得分”这一事件,
表示“甲队总得分大于乙队总得分”这一事件,  ,则可以有
,则可以有
点评:主要是考查了古典概型概率的计算 ,属于基础题。

练习册系列答案
相关题目
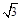 ]上取值,则函数f(x)=ax3+bx2+ax在R上有两个相异极值点的概率是( )
]上取值,则函数f(x)=ax3+bx2+ax在R上有两个相异极值点的概率是( )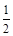
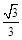
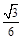
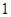 ,
,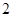 ,
,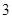 ,
,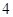 ,
,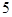 的五张卡片中任取两张,假设每张卡片被取到的概率相等,且每张卡片上只有一个数字,则取到的两张卡片上的数字之和为偶数的概率为( )
的五张卡片中任取两张,假设每张卡片被取到的概率相等,且每张卡片上只有一个数字,则取到的两张卡片上的数字之和为偶数的概率为( )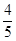
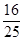
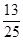
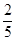
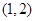 内随机取个实数
内随机取个实数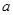 ,则直线
,则直线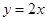 ,直线
,直线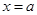 与
与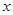 轴围成的面积大于
轴围成的面积大于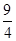 的概率是( )
的概率是( )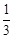
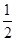
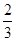
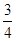
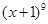 的二项展开式中任取
的二项展开式中任取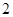 项,
项,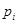 表示取出的
表示取出的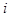 项系数为奇数的概率. 若用随机变量
项系数为奇数的概率. 若用随机变量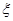 表示取出的
表示取出的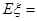 ( )
( )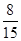
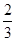
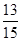
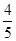
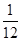 ,
,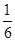 ,
,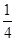 ,
,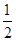 .游戏规则如下:
.游戏规则如下:
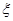 .
.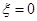 的概率;
的概率;