题目内容
函数f（x）=ln（1-x）的定义域为（ ）
| A、（-∞，1） |
| B、（-∞，1] |
| C、（1，+∞） |
| D、[1，+∞） |
考点：函数的定义域及其求法
专题：函数的性质及应用
分析：根据对数函数的真数大于0建立不等式关系，然后解之即可求出函数的定义域．
解答：
解：要使原函数有意义，则1-x＞0，
解得：x＜1
所以原函数的定义域（-∞，1）．
故选：A．
解得：x＜1
所以原函数的定义域（-∞，1）．
故选：A．
点评：本题考查对数函数的性质和应用，是基础题．解题时要认真审题，仔细解答．
练习册系列答案
周周清检测系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目
阅读如图所示的程序框图，若输入的n是50，则输出的变量S的值是已知tan（π-α）=
，则
=（ ）
| 1 |
| 2 |
| sinα+cosα |
| 2sinα-cosα |
A、
| ||
B、
| ||
C、-
| ||
D、-
|
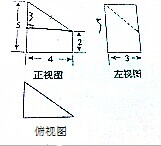某几何体的三视图如图所示，则该几何体的表面积为（ ）| A、54 | B、60 | C、66 | D、72 |