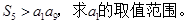题目内容
单调递增数列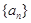 的前
的前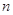 项和为
项和为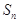 ,且满足
,且满足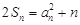 ,
,
(1)求数列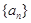 的通项公式;
的通项公式;
(2)数列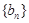 满足
满足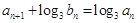 ,求数列
,求数列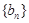 的前
的前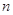 项和
项和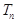 .
.
(1) ;(2)
;(2)  .
.
解析试题分析:(1)由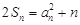 ,先得到
,先得到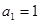 ,当
,当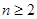 时:
时: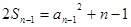 ,得到
,得到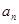 和
和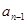 之间关系,
之间关系,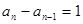 ,故得出
,故得出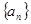 是首项为1,公差为1的等差数列;(2)先由对数式的运算性质求出
是首项为1,公差为1的等差数列;(2)先由对数式的运算性质求出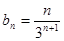 ,然后用错位相减法得到
,然后用错位相减法得到 .
.
试题解析:(1)将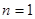 代入
代入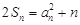 (1) 解得:
(1) 解得: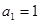
当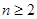 时:
时: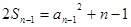 (2)
(2)
由(1)-(2)得: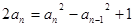 整理得:
整理得: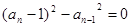
即: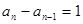 或
或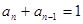 (
(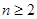 )
)
又因为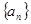 单调递增,故:
单调递增,故: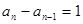
所以: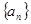 是首项为1,公差为1的等差数列,
是首项为1,公差为1的等差数列,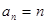
(2)由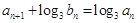
得: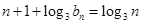 即:
即: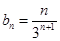
利用错位相减法解得: .
.
考点:1.等差数列通项公式;2.错位相减法;3.对数式的运算性质.

练习册系列答案
相关题目
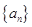 的前
的前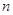 项和为
项和为 ,
,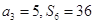 .
. 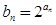 ,求数列
,求数列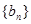 的前
的前 项和
项和 .
.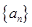 和等比数列
和等比数列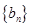 中,a1=2, 2b1=2, b6=32,
中,a1=2, 2b1=2, b6=32, 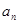 和
和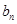 ;
; 中,
中,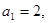 且
且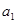 ,
,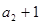 ,
,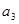 成等差数列,
成等差数列,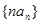 的前
的前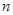 项的和.
项的和.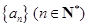 的前
的前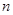 项和为
项和为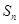 ,且
,且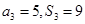 .
.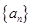 的通项公式;
的通项公式;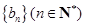 ,若
,若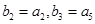 ,求数列
,求数列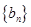 的前
的前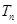 .
.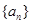 满足:
满足: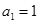 ,
,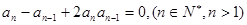
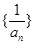 是等差数列并求
是等差数列并求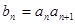 ,求证:
,求证: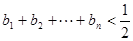 .
.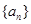 中,
中,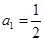 ,点
,点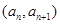 在直线
在直线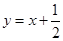 上.
上.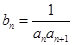 ,求数列
,求数列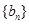 的前n项和
的前n项和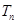 .
.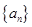 的前四项和为10,且
的前四项和为10,且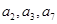 成等比数列
成等比数列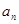
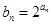 ,求数列
,求数列 的前
的前 项和
项和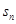
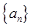 的公差
的公差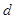 =1,前
=1,前 项和为
项和为 .
.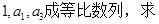
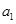 ;
;