题目内容
15.已知复数z满足(1-i)z=i2016(其中i为虚数单位),则复数z的共扼复数$\overline{z}$的对应点在( )| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
分析 把已知等式变形,利用复数代数形式的乘除运算化简,求得$\overline{z}$得答案.
解答 解:由(1-i)z=i2016,
得$z=\frac{{i}^{2016}}{1-i}=\frac{({i}^{4})^{504}}{1-i}=\frac{1}{1-i}=\frac{1+i}{(1-i)(1+i)}=\frac{1}{2}+\frac{1}{2}i$,
∴$\overline{z}=\frac{1}{2}-\frac{1}{2}i$,
则复数z的共扼复数$\overline{z}$的对应点的坐标为($\frac{1}{2},-\frac{1}{2}$),在第四象限.
故选:D.
点评 本题考查复数代数形式的混合运算,考查了复数的代数表示法及其几何意义,是基础题.

练习册系列答案
相关题目
14.已知双曲线的中心在原点,焦点在y轴上,焦距为4,点(1,-$\sqrt{3}$)在双曲线的一条直线上,则双曲线的方程为( )
| A. | y2-$\frac{{x}^{2}}{3}$=1 | B. | $\frac{{y}^{2}}{3}$-x2=1 | C. | $\frac{{y}^{2}}{12}$-$\frac{{x}^{2}}{4}$=1 | D. | $\frac{{y}^{2}}{4}$-$\frac{{x}^{2}}{12}$=1 |
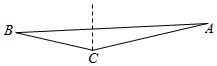 如图,一艘船现在灯塔C北偏东75°的点A且AC=3海里,当船航行了$\sqrt{21}$海里后到达点B,若点B在灯塔C西偏北15°方向上,则B,C两点的距离为$\sqrt{3}$海里.
如图,一艘船现在灯塔C北偏东75°的点A且AC=3海里,当船航行了$\sqrt{21}$海里后到达点B,若点B在灯塔C西偏北15°方向上,则B,C两点的距离为$\sqrt{3}$海里.