题目内容
将圆x2+y2=4上各点的纵坐标压缩至原来的 ,所得曲线记作C;将直线3x﹣2y﹣8=0绕原点逆时针旋转90°所得直线记作l.
,所得曲线记作C;将直线3x﹣2y﹣8=0绕原点逆时针旋转90°所得直线记作l.
(I)求直线l与曲线C的方程;
(II)求C上的点到直线l的最大距离.
(Ⅰ)设曲线C上任一点为(x,y),则(x,2y)在圆x2+y2=4上,
于是x2+(2y)2=4,即 .
.
直线3x﹣2y﹣8=0的极坐标方程为3ρcosθ﹣2ρsinθ﹣8=0,将其记作l0,
设直线l上任一点为(ρ,θ),则点(ρ,θ﹣90°)在l0上,
于是3ρcos(θ﹣90°)﹣2ρsin(θ﹣90°)﹣8=0,即:3ρsinθ+2ρcosθ﹣8=0,
故直线l的方程为2x+3y﹣8=0;
(Ⅱ)设曲线C上任一点为M(2cosψ,sinψ),
它到直线l的距离为d= =
= ,
,
其中ψ0满足:cosψ0= ,sinψ0=
,sinψ0= .
.

 53随堂测系列答案
53随堂测系列答案设x,y满足约束条件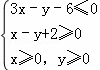 ,若目标函数z=ax+by(a>0,b>0)的最大值为12,则
,若目标函数z=ax+by(a>0,b>0)的最大值为12,则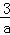 +
+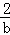 的最小值为( )
的最小值为( )
|
| A. | 4 | B. |
| C. | 1 | D. | 2 |
随机询问某大学40名不同性别的大学生在购买食物时是否读营养说明,得到如下列联表: 性别与读营养说明列联表
| 男 | 女 | 总计 | |
| 读营养说明 | 16 | 8 | 24 |
| 不读营养说明 | 4 | 12 | 16 |
| 总计 | 20 | 20 | 40 |
⑴根据以上列联表进行独立性检验,能否在犯错误的概率不超过0.01的前提下认为性别与是否读营养说明之间有关系?
⑵从被询问的16名不读营养说明的大学生中,随机抽取2名学生,求抽到男生人数 的分布列及其均值(即数学期望).
的分布列及其均值(即数学期望).
(注: ,其中
,其中 为样本容量.)
为样本容量.)
函数f(x)=log2(1+x),g(x)=log2(1﹣x),则f(x)﹣g(x)是( )
|
| A. | 奇函数 | B. | 偶函数 |
|
| C. | 既不是奇函数又不是偶函数 | D. | 既是奇函数又是偶函数 |
定义域为R的偶函数f(x)满足∀x∈R,有f(x+2)=f(x)﹣f(1),且当x∈[2,3]时,f(x)=﹣2x2+12x﹣18.若函数y=f(x)﹣loga(x+1)至少有三个零点,则a的取值范围是( )
|
| A. | (0, | B. | (0, | C. | (0, | D. | (0, |
 展开式中只有第六项二项式系数最大,则展开式中的常数项是( )
展开式中只有第六项二项式系数最大,则展开式中的常数项是( ) ,若
,若 ,则DABC有两组解;
,则DABC有两组解; 则
则
 的图象向左平移
的图象向左平移 个单位,得到函数
个单位,得到函数 =2cos(3x+
=2cos(3x+
 )
) )
) )
) )
) 之间关系最强的是
之间关系最强的是
 是内接于
是内接于 ,
, ,直线
,直线 切
切 ,弦
,弦 ,
, 与
与 相交于点
相交于点 .
. ≌
≌ ;
;
 ,求
,求 .
.