题目内容
设 是等腰三角形,
是等腰三角形, ,则以
,则以 为焦点且过点
为焦点且过点 的双曲线的离心率为( )
的双曲线的离心率为( )
A. | B. | C. | D.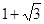 |
B
解析试题分析:根据题设条件可知2c=|BC|,所以|AC|=2×2c×sin600="2"  c,由双曲线的定义能够求出2a,从而导出双曲线的离心率。解:由题意2c=|BC|,所以|AC|=2×2c×sin600=2
c,由双曲线的定义能够求出2a,从而导出双曲线的离心率。解:由题意2c=|BC|,所以|AC|=2×2c×sin600=2 c,由双曲线的定义,有2a=|AC|-|BC|=2
c,由双曲线的定义,有2a=|AC|-|BC|=2 c-2c⇒a=(
c-2c⇒a=( -1)c,e=
-1)c,e= ,选B.
,选B.
考点:双曲线的性质
点评:本题考查双曲线的有关性质和双曲线第一定义的应用

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
直线 与抛物线
与抛物线 所围成的图形面积是( )
所围成的图形面积是( )
| A.20 | B. | C. | D. |
已知曲线C:y=2x2,点A(0,-2)及点B(3,a),从点A观察点B,要实现不被曲线C挡住,则实数a的取值范围是( )
| A.(4,+∞) | B.(-∞,4) |
| C.(10,+∞) | D.(-∞,10) |
双曲线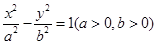 与直线
与直线 有公共点,则双曲线的离心率的取值范围是( )
有公共点,则双曲线的离心率的取值范围是( )
A.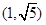 | B.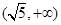 | C.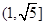 | D.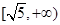 |
以 为中心,
为中心,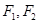 为两个焦点的椭圆上存在一点
为两个焦点的椭圆上存在一点 ,满足
,满足 ,则该椭圆的离心率为
,则该椭圆的离心率为
A. | B. | C. | D. |
若方程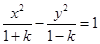 表示双曲线,则实数k的取值范围是 ( )
表示双曲线,则实数k的取值范围是 ( )
A. | B.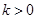 | C.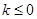 | D.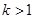 或 或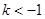 |
若抛物线顶点为坐标原点,对称轴为x轴,焦点在3x-4y-12=0上,那么抛物线方程是( )
A.y =16x =16x | B.y =-16x =-16x | C.y =12x =12x | D.y =-12x =-12x |
已知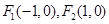 为椭圆
为椭圆 的两个焦点,若椭圆上一点
的两个焦点,若椭圆上一点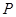 满足
满足 ,则椭圆的离心率
,则椭圆的离心率 ( )
( )
A.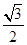 | B.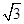 | C. | D. |
 过抛物线
过抛物线 的焦点F,且和
的焦点F,且和 轴交于点A,若△OAF(O为坐标原点)的面积为4, 则抛物线方程为
轴交于点A,若△OAF(O为坐标原点)的面积为4, 则抛物线方程为


