题目内容
若抛物线顶点为坐标原点,对称轴为x轴,焦点在3x-4y-12=0上,那么抛物线方程是( )
A.y =16x =16x | B.y =-16x =-16x | C.y =12x =12x | D.y =-12x =-12x |
A
解析试题分析:根据题意,假设抛物线的标准方程,求得焦点坐标,代入3x-4y-12=0,从而可求抛物线的标准方程解:∵抛物线顶点为(0,0),对称轴为x轴,∴设抛物线方程为:y2=ax,∴焦点坐标为(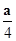 ,0),∵焦点在3x-4y-12=0上,∴3×
,0),∵焦点在3x-4y-12=0上,∴3×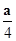 -12=0,∴a=16,∴抛物线的方程为y2=16x,故答案为A
-12=0,∴a=16,∴抛物线的方程为y2=16x,故答案为A
考点:抛物线的标准方程
点评:本题以抛物线的性质为依托,考查抛物线的标准方程,假设抛物线的标准方程是关键

练习册系列答案
相关题目
抛物线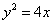 的焦点为F,点
的焦点为F,点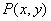 为该抛物线上的动点,又点
为该抛物线上的动点,又点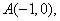 则
则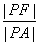 的最小值是
的最小值是
A.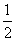 | B.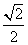 | C.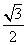 | D.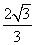 |
设 是等腰三角形,
是等腰三角形, ,则以
,则以 为焦点且过点
为焦点且过点 的双曲线的离心率为( )
的双曲线的离心率为( )
A. | B. | C. | D.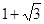 |
椭圆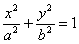
 的离心率是
的离心率是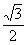 ,则双曲线
,则双曲线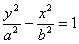 的渐近线方程是( )
的渐近线方程是( )
A.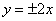 | B.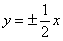 | C.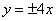 | D.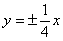 |
已知双曲线 的中心为原点,
的中心为原点, 是
是 的焦点,过
的焦点,过 的直线
的直线 与
与 相交于
相交于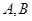 两点,且
两点,且 的中点为
的中点为 ,则
,则 的方程为( )
的方程为( )
A. | B. | C. | D. |
抛物线 的焦点为
的焦点为 ,点
,点 在抛物线上,且
在抛物线上,且 ,弦
,弦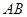 中点
中点 在准线
在准线 上的射影为
上的射影为 的最大值为( )
的最大值为( )
A. | B. | C. | D. |
 为准线的抛物线的标准方程为( )
为准线的抛物线的标准方程为( )
A. | B. | C. | D. |
 后,曲线C变为曲线
后,曲线C变为曲线 ,则曲线C的方程为 ( )
,则曲线C的方程为 ( ) 



 是双曲线
是双曲线 的左焦点,点
的左焦点,点 是该双曲线的右顶点,过
是该双曲线的右顶点,过 轴的直线与双曲线交于
轴的直线与双曲线交于 、
、 两点,若
两点,若 是锐角三角形,则该双曲线的离心率
是锐角三角形,则该双曲线的离心率 的取值范围是( ).
的取值范围是( ).