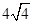题目内容
直线 与抛物线
与抛物线 所围成的图形面积是( )
所围成的图形面积是( )
| A.20 | B. | C. | D. |
C
解析试题分析:由定积分的几何意义,直线 与抛物线
与抛物线 所围成的图形面积是
所围成的图形面积是
 ,故选C。
,故选C。
考点:定积分的计算,定积分的几何意义。
点评:简单题,利用定积分的几何意义,将面积计算问题转化成定积分计算。

练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案
相关题目
已知三个数 构成一个等比数列,则圆锥曲线
构成一个等比数列,则圆锥曲线 的离心率为( )
的离心率为( )
A. | B. | C. 或 或 | D. 或 或 |
已知抛物线 焦点为
焦点为 ,过
,过 做倾斜角为
做倾斜角为 的直线,与抛物线交于A,B两点,若
的直线,与抛物线交于A,B两点,若 ,则
,则 = ( )
= ( )
A. | B. | C. | D. |
中心在原点,焦点在 轴上的双曲线的一条渐近线经过点(4,2),则它的离心率为( )
轴上的双曲线的一条渐近线经过点(4,2),则它的离心率为( )
A. | B. | C. | D. |
设双曲线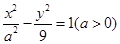 的焦点为
的焦点为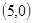 ,则该双曲线的渐近线方程是( )
,则该双曲线的渐近线方程是( )
A.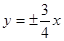 | B.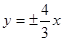 | C.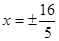 | D. |
正方体  中,
中, 为侧面
为侧面 所在平面上的一个动点,且
所在平面上的一个动点,且 到平面
到平面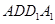 的距离是
的距离是 到直线
到直线 距离相等,则动点
距离相等,则动点 的轨迹为( )
的轨迹为( )
| A.椭圆 | B.双曲线 | C.抛物线 | D.圆 |
抛物线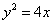 的焦点为F,点
的焦点为F,点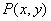 为该抛物线上的动点,又点
为该抛物线上的动点,又点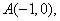 则
则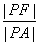 的最小值是
的最小值是
A.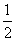 | B.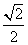 | C.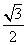 | D.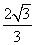 |
设 是等腰三角形,
是等腰三角形, ,则以
,则以 为焦点且过点
为焦点且过点 的双曲线的离心率为( )
的双曲线的离心率为( )
A. | B. | C. | D.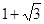 |
 :y="m" 和
:y="m" 和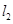 : y=
: y=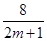 (m>0),
(m>0),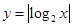 的图像从左至右相交于点A,B ,
的图像从左至右相交于点A,B ,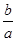 的最小值为
的最小值为 B.
B.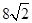 C.
C.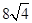 D.
D.