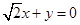题目内容
在平面斜坐标系 中
中 ,点
,点 的斜坐标定义为:“若
的斜坐标定义为:“若 (其中
(其中 分别为与斜坐标系的
分别为与斜坐标系的 轴,
轴, 轴同方向的单位向量),则点
轴同方向的单位向量),则点 的坐标为
的坐标为 ”.若
”.若 且动点
且动点 满足
满足 ,则点
,则点 在斜坐标系中的轨迹方程为
在斜坐标系中的轨迹方程为
A. B.
B.
C. D.
D.
【答案】
D
【解析】
试题分析:解答:解:设M(x,y),∵F1(-1,0),F2(1,0),∴由定义知|MF1|=-[(x+1) +y
+y ],|MF2|=-[(x-1)
],|MF2|=-[(x-1) +y
+y ],因为
],因为 ,那么可知∴(x+1)2+y2+2(x+1)×y×
,那么可知∴(x+1)2+y2+2(x+1)×y× =(x-1)2+y2+2(x-1)×y×
=(x-1)2+y2+2(x-1)×y× ,整理得
,整理得 ,故答案为D。
,故答案为D。
考点:新定义
点评:本题考查新定义,考查轨迹方程等基础知识,考查运算求解能力,属于中档题.

练习册系列答案
相关题目
 定义:平面内两条相交但不垂直的数轴构成的坐标系(两条数轴的原点重合且单位长度相同)称为平面斜坐标系;在平面斜坐标系xOy中,若
定义:平面内两条相交但不垂直的数轴构成的坐标系(两条数轴的原点重合且单位长度相同)称为平面斜坐标系;在平面斜坐标系xOy中,若 如图,在平面斜坐标系中,∠xoy=45°,斜坐标定义为
如图,在平面斜坐标系中,∠xoy=45°,斜坐标定义为 (2008•宝山区一模)如图,在平面斜坐标系中xoy中,∠xoy=60°,平面上任一点P的斜坐标定义如下:若
(2008•宝山区一模)如图,在平面斜坐标系中xoy中,∠xoy=60°,平面上任一点P的斜坐标定义如下:若 中
中 ,点
,点 的斜坐标定义为:“若
的斜坐标定义为:“若 (其中
(其中 分别为与斜坐标系的
分别为与斜坐标系的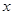 轴,
轴,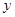 轴同方向的单位向量),则点
轴同方向的单位向量),则点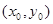 ”.若
”.若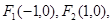 且动点
且动点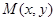 满足
满足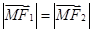 ,则点
,则点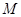 在斜坐标系中的轨迹方程为( )
在斜坐标系中的轨迹方程为( )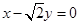 B.
B.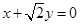 C.
C.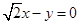 D.
D.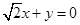
 中
中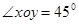 ,点
,点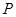 的斜坐标定义为:“若
的斜坐标定义为:“若 (其中
(其中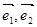 分别为与斜坐标系的
分别为与斜坐标系的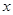 轴,
轴,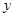 轴同方向的单位向量),则点
轴同方向的单位向量),则点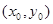 ”.若
”.若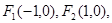 且动点
且动点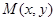 满足
满足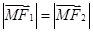 ,则点
,则点 在斜坐标系中的轨迹方程为( )
在斜坐标系中的轨迹方程为( ) B.
B.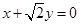
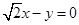 D.
D.